Sur la construction de fonctions de hachage sur les courbes (hyper)elliptiques
Cryptographie
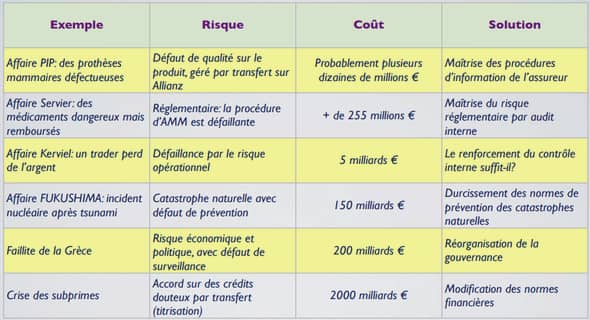
La cryptologie [MVO96] est une science des mathématiques qui étudie la sécurité de l’information et des communications ; elle se subdivise en deux branches : * la cryptographie : une science qui s’intéresse à la conception de schémas et protocoles qui permettent de garantir la sécurité de l’information et des communications en présence d’un potentiel adversaire. Le mot cryptographie vient des mots grecs kryptós qui signifie «caché, secret» et gráfein qui signifie «écrire» ; * la cryptanalyse : une science qui étudie les attaques contre les schémas cryptographiques. Une hypothèse fondamentale en cryptanalyse a été formulée par A. Kerkho
Une note sur l’encodage et le hachage sur les courbes elliptiques et hyperelliptiques
Introduction Pour hacher sur la Jacobienne d’une courbe (hyper)elliptique, nous avons besoin d’une fonction qui associe de manière déterministe un élément d’un corps fini Fq à un point de la courbe. Une telle fonction est appelée un encodage. Nous avons besoin de fonctions d’encodage sur des Courbes (Hyper)Elliptiques pour globalement deux raisons : 1. représentation de points : si un encodage f est presque-injectif (il est injectif quand il est restreint à un certain sous-ensemble de Fq, voir [BHKL13]) et inversible (on peut trouver une antécédent pour n’importe quel élément de l’ensemble des images), il peut être utilisé pour représenter chaque point de l’ensemble des images par une chaîne de bits uniforme aléatoire, comme ce que Bernstein et al. ont fait dans Elligator(1 et 2) [BHKL13]. 2. hachage indi 4. Une note sur l’encodage et le hachage sur les courbes elliptiques et hyperelliptiques 3 ‚ pour le modèle d’intersection de Jacobi (Jacobi Intersection model) au2 ` v2 “ 1, bv2 ` w2 “ 1 : He et al. (2018) [HYW17].
Etat de l’art sur le hachage sur les courbes (hyper)elliptiques
Par une fonction de hachage dans une courbe (hyper)elliptique, nous entendons une fonction H : t0, 1u˚ Ñ JpFqq, qui envoie une chaîne de bits à un élément de la Jacobienne JpFqq de la courbe. Mais pourquoi définir de telles fonctions ? Simplement parce que de nombreux schémas basés sur des courbes elliptiques nécessitent de hacher dans le groupe de points d’une courbe elliptique. Par exemple, Boneh et Franklin [BF01] en 2001 ont été parmi les premiers à exiger un hachage dans les courbes elliptiques .
La Construction H “ f ˝ h1 ` f ˝ h2 [Brier et al.(2010 )] Brier et al. [BCI`10], en utilisant la notion d’encodage admissible, ont montré que la construction Hpmq “ fph1pmqq ` fph2pmqq est indiqué.
1 Introduction et Synthèse de nos travaux |