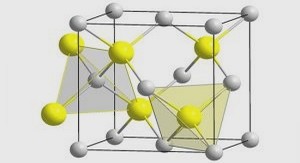
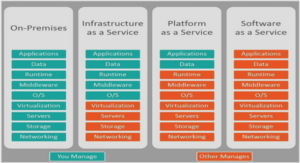
Approximation de haute précision des problèmes de diffraction
Une nouvelle Approximation de Haute Précision
Un schéma numérique de type Volumes Finis garantit une bonne stabilité, une bonne convergence, et n’impose que peu de contrainte sur le choix de la condition CFL. Mais le choix d’approximer la solution par une constante sur chaque cellule n’est pas toujours acceptable. Une bonne méthode généralement utilisée pour monter en ordre est le Galerkin Discontinu. Après calcul des conditions CFL pour un problème d’advection simple monodimensionnel à coecients constants avec diérentes bases polynômiales, nous ferons ensuite une étude de complexité et de coût d’un schéma Galerkin Discontinu en espace et Runge-Kutta en temps dans le cadre général. Prouvant ainsi que ce type de schéma s’avère coûteux, nous présenterons une nouvelle approximation de haute précision qui saura conserver des conditions CFL correctes, dérivée de la méthode des Volumes Finis. 3.1 Méthodes de Galerkin Discontinu : complexité et conditions CFL Soit Ω un segment de R et T ∈ R +\{0}. Considérons comme cas d’étude l’équation d’advection monodimensionnelle : ∀(x, t) ∈ Ω × [0, T], ∂u(x, t) ∂t + a ∂u(x, t) ∂x = f(x, t). (3.1) Soit h ∈ R +\{0} le pas de discrétisation spatiale. Soit (ωk)k∈J1,NK la partition de Ω associée. Chaque ωk est alors un segment [αk, βk] tel que βk − αk = h, et on a Ω = ∪ k ωk. Soit ϕ ∈ C 1 (R) une fonction test. Si u ∈ C 1 (H1 mcx(Ω) × [0, T]), notons uh(x, t) la solution approximée et k ∈ J1, NK. Rappelons la formulation variationnelle (2.48) de Galerkin Discontinu que nous allons utiliser, établie dans la section (2.10.2) pour un système de Friedrichs général en dimension n : Z Ruh∩Rϕ
Etude de la complexité d’un schéma de type RungeKutta couplé à une méthode de type Galerkin Discontinu
Soit r l’ordre du Runge-Kutta et k celui du Galerkin Discontinu. Nous travaillerons sur des équations de types équations des Ondes écrites sous la forme suivante : A0 ∂ ϕ(x, t) ∂t + 2 Xou 3 i=1 Ai ∂ ϕ(x, t) ∂xi = f(x, t). (3.5) Etudier la complexité d’un tel schéma sur une équation aussi générale implique de faire quelques hypothèses. Nous prendrons comme condition CFL celle donnée par le calcul monodimensionnel précédent(3.3) ramenée en bidimensionnel et tridimensionnel par rapport aux conditions CFL des Volumes Finis. Cette hypothèse est d’ailleurs particulièrement optimiste (cf. limites de la méthode de Galerkin Discontinu plus loin). Elle est correcte pour des maillages structurés mais trop favorable pour des maillages déstructurés, où augmenter la dimension de l’espace équivaut à diminuer la condition CFL. On suppose que les inversions des matrices de masses sont stockées. Les calculs seront menés sous deux cas diérents : le premier, où il faut inverser les matrices de masses, le second, où elle seront supposées condensées (cette hypothèse favorisera les grands ordres). Enn, la matrice A0 sera supposée symétrique et ne dépendant pas de paramètres spatiaux (cette dernière hypothèse 136 Une nouvelle Approximation de Haute Précision permet notamment d’assurer qu’il existe une base, celle des polynômes de Legendre, qui convienne pour obtenir des matrices de masses condensées). Calculons le coût d’un schéma Runge-Kutta optimal d’ordre r par élément. Il équivaut du point de vue de la complexité à r résolutions d’un schéma d’Euler Explicite où la première résolution peut être d’une complexité diérente. Soit n le nombre d’inconnues scalaires par élément et p le nombre d’équation du système diérentiel. Soit l’inversion d’une matrice diagonale la référence d’une complexité nulle. Si la matrice de masse est condensée, le coût d’un schéma d’Euler est p fois celui d’une multiplication matrice-vecteur : C1 = p × (2r − 1) n 2 . En revanche, si il faut inverser la matrice de masse, nous aurons un produit matrice de masse-matrice de rigidité, qui induit une complexité en n 3 . D’où un coût en C2 = p × (n 3 + 2(r − 1) n 2 ). Nous allons maintenant mener les études de complexité à partir de ces deux formules.
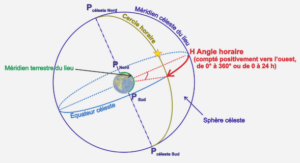
1 Rappels sur les problèmes de propagation d’ondes écrits sous forme de systèmes de Friedrichs |