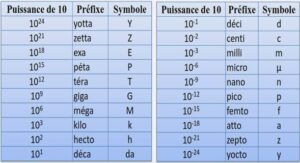
– Historique & Introduction
– Logique des propositions
– Logique des prédicats

Historique & Introduction

Quelques dates de l’histoire de La logique
– En -300 : Aristote (considéré souvent comme le père de la ‘Logique’ comme discipline) définit les concepts de la logique, il divise la logique en 3 parties : l’étude de la conception, du jugement et du raisonnement;
– Leibniz (1646-1713) envisage q’une machine puisse raisonner : enchaîner des propositions élémentaires pour faire des déductions;
– En 1854 : Boole reprend l’étude de Leibniz, il démontre, dans son ouvrage The Laws of Thought (Les lois de la pensée) que tous les processus logiques peuvent être modélisés par des opérations logiques utilisant les opérateurs de base (ET, OU, NON) appliqués à des variables à deux états. Depuis cette date, on peut dire que la logique a migré de la philosophie vers les mathématiques.

Introduction

– La Logique est la discipline qui s’attaque à la notion de validité des raisonnements, toutefois, la manière de traiter cette notion, les fondements,
le formalisme utilisé, etc., changent d’une logique à une autre.
– Nous avons une sorte d’arbre d’héritage entre ces différentes logiques.

Logique des propositions

Introduction
– La logique des propositions est une branche de la Logique et plus précisément de la logique classique.
– Dans la logique des propositions, les opérations qui lient les propositions pour en former d’autres plus complexes sont appelées des connecteurs,
– Un connecteur binaire permet de composer deux propositions pour en obtenir une troisième,
– un connecteur unaire permet d’obtenir une proposition à partir d’une autre.
Langage propositionnel : LP
Définition 4 : Substitution uniforme
– Une substitution (ou substitution uniforme) associe à une variable  propositionnelle p une formule A . Elle est notée [p\A].
– L’application de [p\A] à une formule B , notée B [p\A],est le résultat du  remplacement simultané de toutes les occurrences de p dans B par A.
– B [p\A],est appelé une instance de B.
Théorie des modèles (suite):
Définition 3 : Modèle
– I est un modèle pour une formule A (ou I satisfait A) ssi I(A) = V , noté |=IA.
– I est un modèle pour un ensemble de formules S ssi I est un modèle pour  toute formule A de S.

…..

Si le lien ne fonctionne pas correctement, veuillez nous contacter (mentionner le lien dans votre message)
Introduction à la logique et raisonnements (1757 KO) (Cours PPT)