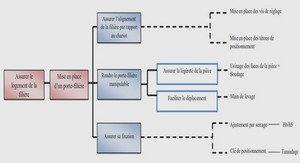
L’imagerie hyperspectral

Principe de l’imagerie hyperspectrale A la difference de la spectroscopie, qui fournit uniquement une mesure spectrale, l’imagerie hyperspectrale int`egre une dimension spatialea la mesure. C’est en quelque sorte l’union des techniques de spectroscopie et d’imagerie. Les donnees hyperspectrales, illustrees sur la Figure 1.11, peuvent ˆetre vues comme une fonction de trois variables : deux variables spatiales x et y donnant la position du pixel dans l’image et une variable spectrale L correspondanta la longueur d’onde de la lumi`ere analysee.A chaque pixel de l’image est associe une signature spectrale, representee generalement par la reflectance (ou encore l’absorbance) en fonction des longueurs d’onde. Ainsi, il est possible d’obtenir la repartition spatiale d’une molecule, d’un materiau ou d’un tissu grˆacea sa signature spectrale unique. Les images hyperspectrales sont donc des donnees agencees en cube. FIGURE 1.11 : Structure d’une image hyperspectrale Image extraite de : [Ravel 17]

Le terme hyperspectral fait reference au nombre de bandes spectrales qu’il est possible d’acquerir sur le spectre electromagnetique. On differencie generalement les images hyperspectrales des images monochromes et multispectrales. Comme nous pouvons le voir sur la Figure 1.12, les images monochromes sont acquises suivant une unique bande spectrale (couvrant une large gamme de longueurs d’onde) et fournissent l’intensite lumineuse mesuree pour chaque pixel de l’image. Les images multispectrales sont acquises sur un faible nombre de bandes spectrales, generalement irreguli`erement espacees (3 en imagerie couleur et ≈ 10 en imagerie multispectrale). Les images hyperspectrales, quanta elles, sont acquises suivant plusieurs centaines de longueurs d’onde, de mˆeme largeur et reguli`erement espacees (on parle communement de bandes spectrales etroites et contigu¨es), permettant d’obtenir un spectre quasi continu pour chaque pixel. Les images hyperspectrales sont acquises par des capteurs de plus en plus performants. Trois caracteristiques principales permettent de quantifier les performances de ces capteurs, et donc, d’evaluer la capacite des donnees obtenuesa restituer l’information du milieu observe :

Balayage spatial

Les methodesa balayage spatial consistenta acquerir en une seule fois toute l’information spectrale d’un ou plusieurs pixels. L’acquisition de la sc`enea imager se fait soit ligne par ligne (methode pushbroom) ou pixel par pixel (methode wiskbroom) en deplac¸ant soit l’imageur soit son champ de vue (FOV pour Field Of View). Le syst`eme d’imagerie whiskbroom utilise un capteur lineaire pour former le cube de donnees. Comme le montre la Figure 1.13, la sc`ene est observee pixel par pixel le long des deux dimensions spatiales et s’effectue par le biais d’un miroir rotatif. La lumi`ere reflechie est ensuite projeteea travers un element dispersif et enregistree sur une barrette CCD, dont chaque cellule corresponda une longueur d’onde. La sc`ene est donc observee point par point selon les deux dimensions spatiales (x et y), ce qui engendre un ensemble de spectresa empiler pour former le cube hyperspectral. La duree d’acquisition d’une sc`ene est generalement longue car le balayage se fait selon chaque dimension spatiale x et y. La technique d’acquisition pushbroom,a la difference de la methode whiskbroom est une technique de balayage lineaire qui permet d’acquerir simultanement la totalite d’une ligne de la sc`ene, ce qui gen`ere une tranche bidimensionnelle de l’image hyperspectrale qui a pour dimension spatiale x et pour dimension spectrale L (Figure 1.14). La lumi`ere reflechie est dispersee sur une matrice CCD et l’ensemble du cube hyperspectral est obtenu en deplac¸ant l’imageur le long de l’autre dimension spatiale y ou alors en deplac¸ant directement les echantillonsa imager sur un convoyeur. Par rapport au syst`eme d’imagerie wiskbroom, le temps d’acquisition de la sc`ene est generalement plus court.

Identifiabilite du mod`ele Reprenons le mod`ele de melange lineaire de l’equation (1.2). Le probl`eme de demelange hyperspectral devient un probl`eme de factorisation de la matrice X en deux matrices S et A. Cependant, si elle existe, cette factorisation n’est generalement pas unique. En effet, considerons une matrice carree inversible Q de dimension R × R. Pour chaque couple (S, A), un nouveau couple (¯S, ¯A) peut ˆetre defini par : ¯S = SQ, ¯A = Q−1A, verifiant lui aussi X = ¯S ¯A . Ainsi, si une factorisation existe, il existe en general une infinite, et donc plusieurs melanges differents peuvent conduire aux mˆemes observations. Le mod`ele de melange spectral est donc non-identifiable. Trouver une solution au probl`eme, i.e. trouver une factorisation de X en un produit de matrices non-negatives, ne garantit aucunement que cette factorisation soit la solution du probl`eme de demelange hyperspectral. D’un point de vue applicatif, cette non-unicite est problematique en termes d’interpretabilite. La contrainte de non-negativite sur les matrices ¯S et ¯A limite le nombre de possibilites pour la matrice de transformation Q et dans certains cas, cette contrainte rend la decomposition unique ; on dit alors que le mod`ele est identifiable.

Formellement, on definit l’identifiabilite du mod`ele lineaire de la fac¸on suivante : Definition 1 [Identifiabilite du mod`ele de factorisation] La factorisation X = SA est identifiable si ∀ ¯S, ¯A tel que X = ¯S ¯A , nous avons : ¯S = SE, ¯A = E−TTA, o`u est une matrice de permutation et E est une matrice diagonale inversible de rang plein avec les elements diagonaux positifs (matrice de misea l’echelle). En d’autres termes, la factorisation est consideree unique si elle l’esta une matrice de permutation et/ou d’echelle pr`es. Les contraintes de non-negativite sur les matrices S et A permettent d’apprehender l’identifiabilite du probl`eme de demelange hyperspectral sous un nouvel angle. En effet, les conditions d’unicite relatives au mod`ele X = SA peuvent s’interpreter de mani`ere geometrique. Tous les spectres xp avec p = 1, …, P peuvent ˆetre representes dans un cˆone convexe : o`u cˆone {S} = _ x ∈ RL|x = S_, _ ≥ 0 represente le cˆone convexe dont les arrˆetes sont les colonnes de S. Il existe une autre interpretation geometrique tr`es utile du mod`ele mais qui necessite, en plus de la non-negativite, la contrainte de sommea 1 des colonnes de la matrice A i.e. AT 1 = 1, o`u 1 est un vecteur compose uniquement de 1. Si cette hypoth`ese est valide, (1.3) peut s’ecrirea nouveau comme : xp ∈ conv {S} , p = 1, …, P, o`u conv {S} = _ x ∈ RL|x = S_, _ ≥ 0, _T 1 = 1 represente l’enveloppe convexe des colonnes de S. Si rang(S) = R, alors les colonnes de S sont les sommets de cette enveloppe convexe. Cette enveloppe est egalement appelee simplexea condition que les colonnes de S soient affinement independantes, i.e., que les vecteurs {sr − sR}r=1,…,R−1 soient lineairement independants. La Figure 1.22 montrent les deux interpretations geometriques possibles.

FIGURE 1.22 : Representation geometrique pour R = 3. Version non normalisee (`a gauche) : cˆone convexe. Version normalisee (`a droite) : simplexe. Les points representent les xp Ainsi, il est evident que le problème de demelange hyperspectral est analoguea la recherche des sommets d’un simplexe. Neanmoins, malgre les contraintes de non-negativite qui restreignent le champs des solutions possibles, les autres formes d’indetermination, que l’on peut assimilera des indeterminations de rotation ne sont pas sans consequences puisqu’elles peuvent mettre en echec le demelange hyperspectral. Considerons S ≥ 0 et A ≥ 0 ; alors xp ∈ RL + ∀p. Ainsi, toute matrice ¯S = [¯s1, …,¯sR] qui satisfait conv {X} ⊆ conv _ ¯S ⊆ RL + est une solution du probl`eme de factorisation de X tel que X = ¯S ¯A , avec ¯A T 1 = 1. La Figure 1.23 illustre l’existence de plusieurs solutions d’un point de vue geometrique.