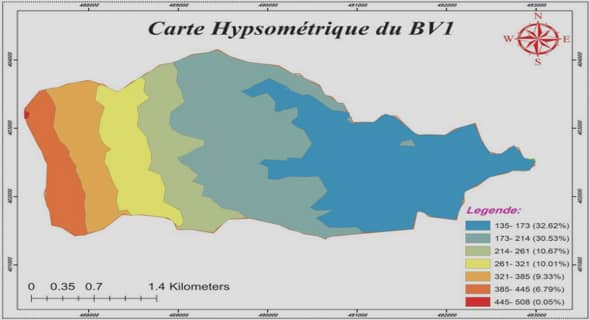
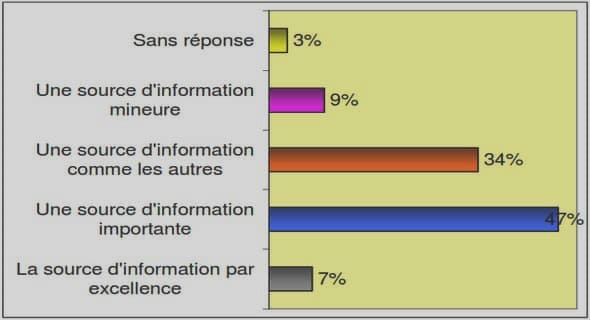
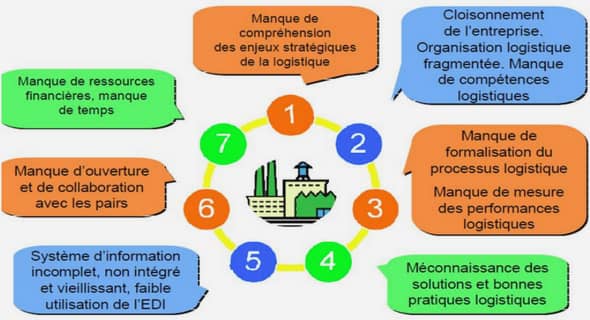
Transferts de Composés Organiques Volatils du sol à l’air ambiant, en passant au travers du béton
Equations à l’échelle microscopique
Equations de conservation de base
En faisant l’hypothèse d’équilibre local (i.e., que l’équilibre thermodynamique est localement vérifié : paramètres intensifs homogènes et constants à cet endroit), nous rappelons les équations de bilan qui traduisent l’évolution de la vitesse et des concentrations du système, en faisant, à l’échelle du pore, l’hypothèse des milieux continus. La mise en place de ces équations est rappelée en annexe B-3. A l’échelle du pore, avec l’hypothèse des milieux continus pour les fluides en présence, les bilans se traduisent par les équations classiques de la cinétique et la dynamique des fluides : Conservation de la masse totale (équation de continuité) : .( ) 0 v t II. 18 Conservation de la quantité de mouvement pour un fluide newtonien incompressible : équation de Navier-Stokes : où Fi est la force extérieure massique exercée sur chaque constituant i.
Equations de transports dans le cas multiconstituants, à l’échelle du pore
Dans notre travail, nous supposerons que l’échelle microscopique est celle où les équations classiques de la mécanique des milieux continus s’appliquent. Plusieurs approches sont proposées dans la littérature pour décrire le problème de convection/diffusion, notamment pour un système multiconstituant. Rigoureusement, les équations de MaxwellStefan (Taylor et Krishna, 1993) sont plus précises, cependant, elles peuvent être écrites dans le cas où le flux est dominé par les gradients de potentiel chimique (Quintard et al., 2006) comme qui permet d’écrire le flux de diffusion pour un constituant comme une « loi de Fick généralisée ». Nous adopterons cette formulation par la suite. Cependant, pour des systèmes non isothermes, un gradient de température apparaît dans les équations de MaxwellStefan. Ceci induit un couplage complexe entre transport de masse et transfert thermique, appelé thermodiffusion. Ce phénomène pourrait être important près de la surface du sol où les oscillations diurnes et saisonnières de température influencent le transport dans les couches superficielles du sol et les échanges avec l’atmosphère. Néanmoins, nous négligerons ce phénomène par la suite. D’autre part, les équations II.18 et II.19 sont valables quand les collisions molécule-molécule sont bien plus fréquentes que les collisions molécule-paroi du pore, c’est bien le cas dans un milieu comme notre sable. Nous avons choisi, par souci de clarté, de détailler les opérations du changement d’échelle pour un cas simplifié, où sorption et autres échanges interphases sont négligés (« Cas 0 »). Puis nous précisons les effets de la prise en compte des phénomènes d’échanges multiphasiques pour les cas « sable sec » et « sable humide ». Cas 0 : convection-diffusion simple – milieu inerte Dans un milieu poreux, à l’échelle du pore, pour un mélange à N constituants, et deux phases notées α (fluide, liquide ou gaz) et β (solide), en négligeant les phénomènes de sorption, ainsi que les réactions de dégradation, le transport de chacun des constituants est régi par la loi de Fick généralisée (conservation des espèces):où la présence d’une interface α-β, rigide, dans le milieu se traduit par une condition aux limites : où ωiα est la fraction molaire en constituant i dans la phase , qui est le rapport entre le nombre de moles de molécule du constituant sur le nombre total de moles dans la phase ; et v est la vitesse massique moyenne, définie par : Nous avons utilisé ici l’expression pour le flux de diffusion du constituant qui est appelée loi de Fick généralisée. Il est nécessaire de résoudre simultanément tous les bilans d’espèces, étant donné que le flux d’un constituant dépend du flux des autres constituants. Mais notons que seuls N-1 bilans sont nécessaires (seulement N-1 équations de diffusion indépendantes) en sus du bilan de masse total, la fraction massique du dernier constituant pouvant être déduite des précédentes. Les coefficients de diffusion massique Dij de la loi de Fick généralisée sont définis par écriture matricielle, (cf. Quintard et al., 2006 b) en fonction des coefficients de diffusion binaires Dij, des coefficients d’activité, et des fractions massiques et molaires. Donc finalement, les N équations de bilan de masse peuvent être exprimées comme : Et pour conditions limites, à l’interface (α-β),.nous avons: CL1 : . 0 1 1 N j nαβ Dij j sur Aαβ II. CL2 : nαβ.( v ) 0 sur Aαβ II. Les équations II. 27 et II. 28, seront utilisées comme équations de départ pour le développement du changement d’échelle par prise de moyenne volumique.
Cas 1 : Milieu sec avec sorption
Les équations applicables au cas 1 sont presque les mêmes que celles du cas 0, en prenant en compte les quelques modifications décrites ici, et en considérant, pour ce cas, que la phase fluide est gazeuse, notée α et la phase solide, notée ici γ (donc en remplaçant les indices β du cas 0 par γ), comme illustré par la Fig.II. 5. Fig.II. 5 : Schéma d’un milieu poreux sec (sable par exemple), et de son VER (V ) Nous prenons maintenant en compte les phénomènes de sorption. Comme nous l’avons vu, dans le sable sec, la sorption peut être décrite par une isotherme linéaire. En prenant en compte les phénomènes de sorption, la condition limite II. 1 1 . nαγ Dij sur Aα-γ II. où ad i est la fraction massique de constituant i adsorbé sur la surface Aαγ, encore appelée fraction massique surfacique ; elle est reliée à la fraction massique de façon linéaire (dans notre cas), par le coefficient de sorption sur la phase γ, Keq iγ : ad i Keqii II.
Cas 2 : Milieu humide
Dans un milieu contenant de l’eau, par exemple un sable à saturation résiduelle en humidité (HR=13%), une troisième phase intervient : la phase aqueuse β. Cette phase est immobile, et se situe, comme sur la Fig.II. 6, autour des grains de sable. Chapitre II : Eléments théoriques sur les transferts en milieu poreux Fig.II. 6 : Schéma d’un sable à saturation résiduelle, et de son VER (V ) Il a été démontré (Kim et al., 2001), qu’à partir d’une saturation en eau de 3%, toute la surface des grains de sable (sable correspondant à celui de notre étude) est recouverte d’une couche d’eau continue, ce qui empêche tout contact direct entre la phase gazeuse et la phase solide. Il n’y a donc pas de phénomène de sorption directe de la phase gazeuse sur le milieu poreux, mais la sorption a lieu par l’intermédiaire de la phase aqueuse. Par contre, la présence de la phase β engendre des phénomènes d’échanges entre la phase gazeuse et aqueuse, que nous allons devoir décrire : un phénomène de rétention au niveau de l’interface, qui engendre un retard et que nous assimilerons à de la sorption, et un phénomène d’échange, qui engendre un terme puits/source. Donc dans ce cas, deux équations sont nécessaires afin de décrire le transport d’un constituant i dans notre système multiphasique : une équation décrivant la convection/diffusion en phase gazeuse, avec ses échanges avec la phase aqueuse, et une équation décrivant la diffusion en phase aqueuse avec ses échanges avec les phases gazeuse et solide.
RESUME EN FRANÇAIS |