1. Le calcul du produit scalaire de deux vecteurs réels u et v de dimension
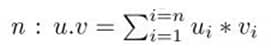
Produit_scalaire (u: Tableau d’entiers, v: Tableau d’entiers n:entier):entier
VAR i, prod_scalaire : entiers
Début
prod_scalaire <- 0
Pour i <- 1 a n Faire
prod_scalaire <- prod_scalaire +u[i]*v[i]
Fin pour
Retourner prod_scalaire;
Fin
2. Ecrire l’algorithme qui calcule le produit de deux matrices carrées réelles
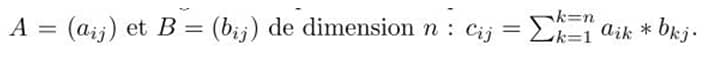
Produit_matriciel (a: Matrice carrée, b: Matrice carrée, n: entier): Matrice carrée
VAR c: Matrice carrée *n
i: entier
Début
Pour i <- 1 a n Faire
Pour j de 1 a n Faire
c[i][j] <- 0
Pour k de 1 a n Faire
c[i][j]<- c[i][j] + a[i][k]* b[k][j]
Fin pour
Fin pour
Fin pour
Retourner c
Fin
3. Ecrire un algorithme qui calcule le plus grand écart dans un tableau (l’écart est la valeur absolue de la déférence de deux éléments).
VAR : min, max, i: entiers
Début
min = t[1]
max = t[1]
Pour i <- 2 a n Faire
Si t[i] > max
Alors
Max = t[i]
Fin si
Si t[i] < min
Alors
Min = t[i]
Fin si
Fin pour
Return max – min
Fin
4. Le calcul de la moyenne et du minimum des éléments d’un tableau
VAR somme, i: entiers
Moyenne : réel
Début
Somme <- 0
Pour i <- 1 a N Faire
Somme<- somme + T[i]
Fin pour
Moyenne <- somme / N
Retourner Moyenne
Minimum(T: Tableau d’entier, N: entier):entier
VAR min, i: entiers
Début
min <- T[1]
Pour i <- 2 a N Faire
Si T[i]<min< p= » »>
Alors min =T[i]
Fin si
Fin pour
Retourner min
Fin