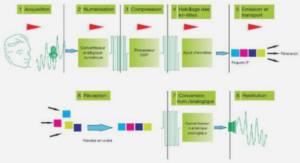
Mise en relief des notions à enseigner

Des décalages entre le savoir savant, le savoir à enseigner et le savoir enseigné 2.1 Les cadres Dans nos analyses historique et curriculaire, nous avons montré que les notions de géométrie analytique spatiale s’insèrent dans un ensemble plus large de notions dont font partie l’algèbre et la géométrie (synthétique et vectorielle).

En particulier, l’articu-lation des différents cadres est très différente dans l’enseignement étudié par rapport à celle dans le savoir savant et le savoir à enseigner. En effet, l’émergence historique de la géométrie analytique apparait comme une unification des domaines géométrique et algébrique ce qui amène une nouvelle formalisation des équations. C’est également le cas dans le savoir à enseigner dans lequel l’algébrisation de la géométrie est de plus en plus présente au fur et à mesure de la scolarité. Dans l’enseignement étudié, ces caractères unificateur et formalisateur de la géométrie analytique n’apparaissent pas. Nous supposons qu’il y a deux explications à ce décalage. Tout d’abord, un des objectifs du cours est d’assurer la transition secondaire-université. De ce fait, les notions qui y sont abordées ont déjà fait l’objet d’un enseignement préalable. Il ne s’agit donc pas de reproduire tout le développement des notions mais bien de revenir sur certaines notions essentielles pour bien débuter les autres cours universitaires tel que l’algèbre linéaire.

Ensuite, nous pensons que cela nécessite d’introduire un chapitre de géométrie synthétique dans le cours dont il est question ici afin de bien mettre en avant ces aspects. Or, au vu de la durée du cours de Mathématiques élémentaires et du peu d’utilisation de cette géométrie pour la suite du cursus, il nous semble pertinent que l’enseignement ne choisisse pas de les aborder. De plus, l’articulation des cadres géométriques n’apparait pas de la même façon tant dans l’enseignement étudié que dans l’histoire ou les programmes. L’étude historique révèle que la géométrie est purement synthétique jusqu’en 1637. Vient ensuite la géométrie analytique (plane et spatiale) notamment avec les travaux de Descartes et Fermat.

La géométrie vectorielle émerge en dernier suite à une critique de Leibniz. Il reprochait à la géométrie analytique d’être trop algébrique et de ne plus être liée au problème géométrique étudié. Möbius donne alors une première description des droites et des plans en termes vectoriels pour pallier cette critique. Ainsi, la géométrie vectorielle apparait comme la méthode géométrique permettant de lier la géométrie synthétique et la géométrie analytique. Bien que d’un point de vue chronologique les cadres géométriques n’émergent pas dans cet ordre, notre étude historique montre qu’il est mieux d’aborder la géométrie synthétique, puis la géométrie vectorielle et enfin la géométrie analytique. C’est ce cheminement qui est suivi dans les programmes actuels. Dans l’enseignement étudié, nous avons montré que ce n’est pas le cas et que les jeux de cadres se limitent à la géométrie vectorielle et analytique.

Les registres

Au niveau des registres, nous avons repéré des décalages importants entre les trois savoirs. L’enseignement étudié met en jeu les registres du dessin, graphique, de la langue naturelle, algébrique, ensembliste et de la logique. Or, les notions de logique et de théorie des ensembles sont beaucoup trop modernes par rapport à la période de l’histoire que nous avons retracée. Ils n’apparaissent donc pas dans notre analyse historique. L’étude du savoir à enseigner met quant à elle clairement en avant les registres algébrique et de la langue naturelle. Les registres ensembliste et de la logique peuvent également apparaitre grâce aux nouveaux programmes puisqu’il est demandé de travailler ces notions au gré des besoins.

Les points de vue

Le décalage le plus flagrant, pour nous, concerne les points de vue. Chronologiquement parlant, le point de vue cartésien est le premier à émerger dans l’histoire des mathématiques retracée au chapitre III. Ensuite, le point de vue paramétrique, dans le cadre de la géométrie vectorielle, est apparu grâce au calcul barycentrique. Il faut attendre que la notion de rang soit définie par Frobenius pour que le point de vue paramétrique apparaisse dans le cadre de la géométrie analytique et s’articule avec le point de vue cartésien. Or, la notion de rang ne survient qu’après avoir considéré les équations et les solutions d’un système comme des n-uplets. De la sorte, l’histoire montre que les points de vue sont articulés entre eux.

Or, cette articulation n’est pas du tout évoquée dans les programmes et se résume bien souvent au sens paramétrique/cartésien dans l’enseignement étudié. De plus, la notion de rang n’apparait pas dans le savoir à enseigner et dans le savoir enseigné. Cela ne permet pas de donner des moyens de contrôle aux apprenants quant au nombre de vecteurs et de paramètres à utiliser. Cependant, les trois aspects du rang apparaissent implicitement dans les nouveaux programmes. Ce qui nous laisse supposer qu’une articulation est désormais possible.