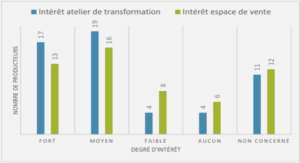
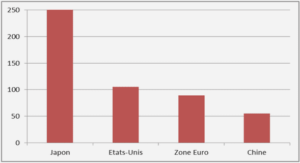
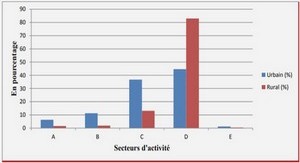
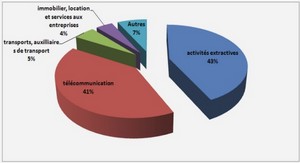
Depuis longtemps, plusieurs nombres de scientifiques, chercheurs et/ou ingénieurs dans le domaine de génie électrique ont travaillé sur l’énergie renouvelable, plus précisément de l’énergie provenant des modules photovoltaïque dans le but d’améliorer les rendements obtenus et de trouver d’autre modèle pour renforcer leurs performances.
Avec le changement climatique actuel, il est devenu de plus en plus difficile de faire des études sur le domaine photovoltaïque. Ces évolutions engendrent de nombreux problèmes d’analyse et de dimensionnement. D’où le choix de notre étude concernant une démarche de modélisation et d’analyse basée sur les systèmes d’ordre non entier appelés « systèmes d’ordre fractionnaire ». Avec ces systèmes nous pouvons travailler avec la théorie fractale, qui est une théorie qui met en évidence le caractère d’ordre non entier de tout système présentant une ramification ou une invariance d’échelle, dans le domaine du système photovoltaïque.
Par définition, fractales représentent les objets dont leurs formes sont irrégulières et ils sont présentés de façon universelle dans la nature et mieux comprendre notre environnement. De même que la théorie fractale est une théorie mathématique, l’application de la théorie fractale commence à trouver de la place dans nos vies quotidienne, surtout dans le domaine de la science, de visualiser des concepts abstraits, et de faire des prévisions.
GENERALITES SUR LA THEORIE FRACTALE
Beaucoup de mathématiciens et de scientifiques ont déjà entendu le mot «fractale» mais la plupart ne savent vraiment de quoi il s’agit. Ce nom méconnu signifie à la fois « brisé » et « irrégulier ». Cette théorie sert à représenter géométriquement des objets qui ont des formes souvent irrégulières. Ces objets présentent des éléments discernables sur une large gamme d’échelles et dont les parties ont approximativement la même structure que le tout
Géométrie fractale
Historique des fractales
Le concept fractal est devenu en vogue aujourd’hui grâce à des nombreuses applications. Dans les années 70 que Benoit Mandelbrot invente le nom fractal et devenu aujourd’hui la référence à la géométrie de la nature. Il existe quelques définitions qui ont vu le jour à l’époque ou la communauté scientifique fait pression: «Un ensemble fractal (dans le plan ou dans l’espace) est un ensemble dont la dimension de Hausdorff (ou dimension fractale) est strictement supérieure à sa dimension topologique». Lorsqu’on parle de la géométrie fractale, on pense toujours à la géométrie de la nature. Et, elle est omniprésente dans notre environnement. Cependant, on peut se demander quelles ont été les premières images fractales crées artificiellement par des hommes.
Premières ébauches des images fractales
Les premières ébauches d’images selon la documentation viennent d’Apollonius de Perge et remontent à trois siècles avant J-C. Dans son livre Tangencies, ce disciple d’Euclide démontra comment tracer un cercle tangent à trois autres objets qui sont soit des points, des lignes ou des cercles. Ainsi, il utilisa ce résultat pour construire une figure qui sera reprise plus tard par Mandelbrot en tant qu’image fractale. Sa construction consiste à prendre un triangle curviligne (dont les cotes sont des arcs de cercles). On peut alors trouver un cercle inscrit à l’intérieur. Cette étape créer trois nouveaux triangles curvilignes dans chacun desquels on peut inscrire un autre cercle. En continuant ce procédé et jusqu’à l’infini, on trouve une image appelée la baderne d’Apollonius.
De plus, le philosophe et mathématicien Leibniz a introduit la notion d’autosimilarité en 1700 sur les images fractales. La majorité des fractales respectent cette propriété et qui explique le fait qu’une figure est dite autosimilaire si celle-ci préserve une certaine symétrie interne en dépit des variations d’échelle.
Ensuite, en 1520 le pentagone de Dürer est apparu le jour . Sa construction est expliquée dans le manuel de géométrie Instructions pour la mesure, à la règle et au compas, des lignes, plan et corps solides écrit par l’artiste allemand Albretch Dürer. Son image fractale consiste en un pentagone régulier dans lequel on place six petits pentagones congrus ; cinq d’entre eux doivent recouvrir les angles du pentagone de façon à ce que les côtés adjacents correspondent et le dernier pentagone doit se situer au centre du grand pentagone mais en ayant subi une rotation de 180° par rapport à celui-ci. En reprenant ce processus pur chacun des nouveaux pentagones et ainsi de suite, on trouve une image ressemblant à une dentelle.
En 1904, Von Koch, proposa une construction extrêmement simple aboutissant à une courbe continue qui n’a pas de tangente. Pour y arriver, on prend un segment de longueur l et on remplace son tiers central par un « pic » formé de deux segments de longueur l/3. On refait le même processus pour chacun des quatre nouveaux segments et ainsi de suite. A l’infini, on obtient une courbe exclusivement formée de « pics » qui on le sait, n’admettent pas de tangente.
Classification des objets fractals
Les objets fractals peuvent être classés en trois catégories selon sa nature et ses procédés de construction. D’abord, nous regardons les fractals aléatoires lorsque les objets en questions ne sont pas générés par des mécanismes déterminismes mais par des processus aléatoires. On peut dire que toutes les fractales dites « naturelles » ou paysages fractals font partie de cette catégories, c’est à dire les phénomènes naturelles ou artificielles ont une structure fractale.
Ensuite, les fractales construites à partir de systèmes de fonctions itérées (procédé mathématique permettant de définir un certain nombre de transformations Modélisation fractale des réseaux électriques géométriques affines) sont placées en seconde catégorie. La règle de construction repose ainsi sur un remplacement géométrique fixe : d’une itération à une autre, on remplace chaque élément par un autre, identique pour tous. A titre d’exemple, cette famille regroupe l’ensemble de Cantor, le triangle ou tapis de Sierpinski, le flocon de Koch, … etc. C’est généralement cette famille d’objets fractals qui présente une propriété d’autosimilarité.
Enfin, la troisième catégorie englobe les fractales construites à partir d’une relation de récurrence en chaque point dans l’espace. On retrouve dans cette catégorie les ensembles de Julia et de Mandelbrot ainsi que les fractales de Lyapunov.
Dimension topologique
D’après une définition mathématique, deux objets sont équivalents topologiquement s’il est possible de déformer l’un vers l’autre à l’aide d’un homéomorphisme : transformation bijective et continue (qui préserve la connexité) . Ainsi, la dimension topologique d’un objet devrait être préservée sous une transformation homéomorphique et les valeurs admises sont des entiers. Poincaré a proposé une définition semblable à celle d’Euclide d’une telle dimension. Posons d’abord le vide de dimension -1.
Puis, on procède par induction : si un objet connexe peut être divisé en deux (ou plusieurs) objets disjoints en lui retirant une partie de dimension n (et qu’il n’est pas possible de le faire avec une partie de plus petite dimension) alors on dit qu’il est de dimension n + 1.
Ainsi, un point ne peut pas être brisé en plusieurs morceaux donc, il est de dimension −1+1 = 0. Par ailleurs, un nombre fini de points est totalement non connexe et reste de dimension 0. Une ligne peut être brisée en deux lignes disjointes si on lui retire un point qui est de dimension 0, donc la ligne est de dimension 0 + 1 = 1. Et ainsi de suite.
Enfin, bien que Peano et Hilbert aient réussi à déformer l’intervalle [0, 1] en un carré, leurs transformations n’étaient pas des homéomorphismes (elles n’étaient pas injectives) par conséquent, il n’y a pas de contradiction en affirmant que la dimension topologique de l’intervalle soit 1 alors que celle du carré soit 2.
En géométrie euclidienne, la dimension d’un objet est égale au nombre de paramètres (définissant une unité de mesure) nécessaires pour le décrire. La dimension d’un droit est ainsi égale à 1, puisqu’un seul paramètre, c’est-à-dire la distance entre une origine choisie et un point de cette droite, permet de la caractériser. Une figure quelconque dans le plan, quant à elle une dimension est égale à 2, puisque tout point de cette figure est décrit par 2 paramètres (une abscisse et une ordonnée). Nous qualifierons par la suite cette dimension de topologique. Afin de mesurer une longueur, une surface ou un volume, une méthode employée consiste à recouvrir ces ensembles de pavés dont la longueur, la surface ou le volume peuvent être considérés comme une unité de mesure.
INTRODUCTION |