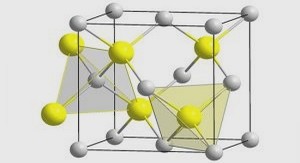
Transport électronique et Verres de Spins

 The Anderson localization in quasi one dimensional systems

What is Anderson localization?

In 1958 Anderson [111] proved that diffusion in random lattices can disappear due to the quantum interferences. For a three dimensional system, a transition between a metallic and an insulating regime appears when the strength of disorder is increased. For large disorder, electrons cannot escape the system, they are localized in a region of the solid: this is the Anderson localization. In an electronic transport point of view, Anderson localization is characterized by a vanishing conductance, as the electrons have difficulties to escape the solid. On the contrary, the conductance is large in the metallic regime. In the following more quantitative characterizations of the Anderson localized state will be highlighted. In 1979, Abrahams et al. [120] established a scaling theory of localization stating the absence of quantum diffusion in one and two dimensions. Their argument is presented briefly in the following. They assume the existence of a single parameter scaling that describes the behavior of electronic transport when the typical size L of the system is modified. This single parameter is the dimensionless conductance g(L) 1 . In other words, they assume: g(bL) = f(b, g(L)), (5.1) where b is a scaling factor. In continuous terms, it is practical to define a scaling function β(g) by: β(g) = d log g d log L . (5.2) At large and small conductance, it is possible to deduce the asymptotics of that function from general arguments. Large conductance In that case, macroscopic transport can be used, the quantum effects are negligible (the effects of disorder are small). We use then the relationship between the conductance and the conductivity σ (because the conductivity does not depend on L), and for a sample of size L d (where d is the dimension of the sample), we get G(L) = σLd−2 . We deduce then: limg→∞ β(g) = d − 2. (5.3) 1we remind the reader that g = G/G0, where G is the conductance of the system and G0 the quantum of conductance defined in section 3.2.2.

 THE ANDERSON LOCALIZATION 

Small conductance In the limit of small conductance, all electronic states are predicted to be exponentially localized around the impurities, and therefore g falls off also exponentially (at least at zero temperature): g = g0e −αL . (5.4) From this relation, we deduce the behavior of the scaling function in that regime: β(g) = log g − log g0 (5.5) at all dimensions. The scaling function From these limits, the authors sketched the universal curve β(g) reproduced in figure 5.1, using continuity arguments. The flow of renormalization (by increasing at each step the size of the Figure 5.1: Plot of the scaling function as a function of log g for one, two and three dimensional systems. The absence of fixed points for a finite value of conductance in one and two dimensions leads to the absence of metallic regime in the asymptotic limit. Extracted from [120]. system) tends to g(Lx → ∞) = 0 in one and two dimensions, as the sign of the β function indicates the increase or decrease of the conductance with the length of the system. The presence of a fixed point in three dimensions ensures the existence of a transition at g = gc. Recently, the possibility to probe directly the properties of this localization with cold atoms [121, 122] has greatly renewed interest for this physics. In the case of quasi one dimensional wires with a fixed amplitude of disorder, the conductance vanishes with increasing longitudinal length Lx. For short wires, the conductance can reach large values as shown on figure 5.2. Changing the length of the sample allows the system to reach both metallic and insulating regimes of conduction. The goal of this chapter is to study these regimes and in particular the conditions to enter the diffusive metallic behavior, which is the relevant experimental regime of usual nanowires.

 Universal and non universal regimes

As we have seen in chapter 3 (section 3.2.5), systems with longitudinal length Lx much larger than the magnetic length Lm are in GOE and systems of length much smaller than Lm are in GUE. Each of these ensembles defines a different universality class, as both ensembles are characterized by different symmetries. Experimentally speaking, real spin glass nanowires are generally neither in one class nor in the other, but in a non universal regime, which corresponds to the case of moderate values of magnetic disorder J or of a longitudinal length in between the two limits described above. In the following we will study both the universal and the non universal properties of transport in the insulating and metallic regimes of conduction. 5.2 Study of universal properties of the Anderson localized regime 5.2.1 The localization length In a metallic nanowire with a given value of disorder, there exists a value of the longitudinal length for which the average conductance becomes smaller than one, as explained before. Figure 5.2 shows this behavior for a purely metallic wire and for a spin glass wire with different values of magnetic disorder J. This curve illustrates our point that the conductance of a wire vanishes 0 1000 2000 3000 4000 5000 6000 0 1 2 3 4 5 L x 〈 g 〉 L y = 10 J = 0 J = 0.05 J = 0.1 J = 0.2 J = 0.4 Figure 5.2: Evolution of average conductance with longitudinal length Lx for different values of magnetic disorder. The line hgi = 1 is shown, to emphasize that for large systems, the wire acquires vanishingly small values of conductance. with increasing length. As shown in section 5.1 in the regime of small conductance, exponential localization occurs which implies that the conductance is exponentially decreasing: equation (5.4). Using dimensional arguments, α −1 is the decaying length of the conductance. It is natural  to assume that this length is directly proportional to the so called localization length ξ which characterizes the cross-over between the metallic (Lx < ξ) and the localized (Lx > ξ) regimes. In this section, we present two methods to determine this length via transport properties. The determination of ξ First we consider the typical conductance of the system defined as: gtyp = e hlog gi . (5.6) From the above discussion (see equation (5.4)), we expect the following scaling behavior: gtyp ∼ e − 2Lx ξ for Lx ≫ ξ (5.7) Knowing equation (5.7) we plot the average value of the logarithm of the conductance as a function of the longitudinal length of the sample. This is shown in figures 5.3, 5.4 and 5.5, for different values of magnetic disorder. These curves show that for very small longitudinal lengths 0 0.5 1 1.5 2 x 104 −6 −4 −2 0 2 4 L x 〈 log g 〉 J=0 L y =10 L y =20 L y =30 L y =40 Figure 5.3: Evolution of hlog gi = log gtyp as a function of longitudinal size for different transverse lengths. The amplitude of magnetic disorder is J = 0. The linear part of the curve allows one to get the localization length from the scaling form in the insulating regime hlog gi = − 2Lx ξ . hlog gi is not proportional to Lx. For large values of the longitudinal length, hlog gi is directly proportional to Lx as expected and a basic fit of this linear part of the curve gives access to the localization length. Notice well that the linear part in all these curves is clearly identified, so the evaluation of ξ is straightforward. This method allows to determine the localization length for each value of Ly and J we consider. Another way to extract the localization length from the conductance consists in studying the Lyapunov exponent γ of the transfer matrix of the system. In the scaling theory of localization (RMT), a Lyapunov exponent can be defined related to the product of transfer matrices [123, 124, 125, 101] (see section 3.2.5 for the definition of the transfer matrix). Consider the transfer matrix Θ of the entire wire. It is a product of random matrices (each of size 2N × 2N) as: Θ = Yn a=1 Ta. (5.8) 76 CHAPTER 5. UNIVERSAL PROPERTIES OF CONDUCTION 0 2000 4000 6000 8000 10000 12000 −3 −2 −1 0 1 2 3 L x 〈 log g 〉 J = 0.05 L y = 5 L y = 10 L y = 15 L y = 20 Figure 5.4: Evolution of hlog gi as a function of longitudinal size for different transverse lengths and J = 0.05. The linear part of the curve allows one to get the localization length from the scaling form in the insulating regime hlog gi = − 2Lx ξ . 0 2000 4000 6000 8000 10000 12000 −5 −4 −3 −2 −1 0 1 2 3 L x 〈 log g 〉 J = 0.4 L y = 5 L y = 10 L y = 15 L y = 20 Figure 5.5: Evolution of hlog gi as a function of longitudinal size for different transverse lengths and J = 0.4. The linear part of the curve allows one to get the localization length from the scaling form in the insulating regime hlog gi = − 2Lx ξ . In the limit of large wires (n → ∞), the 2N random eigenvalues e ±2xi of ΘΘ† tend to the non-random values e ±2γiLx , with γi independent of Lx [101]. The largest Lyapunov exponent is equal to this inverse of the localization length.

UNIVERSALITY IN THE LOCALIZED REGIME 

Following [126, 116] it is a function of the conductance: γ(Lx) = 1 2Lx log  1 + 1 g(Lx)  −→Lx→∞ 1 ξ . (5.9) On figure 5.6 and 5.7 we have plotted the Lyapunov exponent versus the inverse of the longitudinal length for different values of magnetic disorder. Different curves correspond to different widths of the wire. The advantage of this method is that there is no need of any numerical fitting 10−4 10−3 10−2 10−1 0 1 2 3 4 5 6 x 10−3 L x −1 γ L y = 10 J = 0 J = 0.05 J = 0.2 ξ J = 0.4 prev Figure 5.6: Evolution of Lyapunov exponent with the inverse of longitudinal length in semi-log plot. Circles correspond to J = 0, squares to J = 0.05, diamonds to J = 0.2 and triangles to J = 0.4. The value of the transverse length is 10. The localization length can be extrapolated from the value of γ for Lx → ∞. The denomination ξprev is the value of the localization length determined previously using the typical conductance. The different values correspond to the different values of magnetic disorder in consideration. procedure, only an extrapolation is necessary to get the value of the inverse of the localization length for an infinite wire. Nevertheless, this method has less accuracy than the previous one (with the use of the typical conductance) as on many plots of figures 5.6 or 5.7, the Lyapunov exponent is still significantly varying with the longitudinal length. To reduce the error, very long wires are needed2 , which is limited by calculation time. Both methods give finally comparable results but the accuracy on the localization length is better with the first method using the typical conductance, as for all geometries and all values of magnetic disorder a linear behavior of the average of the logarithm of conductance has settled. On all these curves one obviously notice that the localization length depends on both the magnetic disorder J and the width of the sample. The next section deals with the study of the behavior of ξ as a function Ly, plotted for different values of magnetic disorder. The evolution of ξ with the width of the wire Qualitatively the localization length is a growing function of the width of the wire as the entrance in the insulating regime corresponds to the progressive closure of all propagating modes whose 2compare for instance figure 5.6 and 5.7: in the first one, the maximum aspect ratio is 3 000, whereas it is only 600 in the second one.  Figure 5.7: Evolution of Lyapunov exponent with the inverse of longitudinal length in semi-log plot. Circles correspond to J = 0, squares to J = 0.05, diamonds to J = 0.2 and triangles to J = 0.4. The value of the transverse length is 20. The localization length can be extrapolated from the value of γ for Lx → ∞. The denomination ξprev is the value of the localization length determined previously using the typical conductance. The different values correspond to the different values of magnetic disorder in consideration. number is directly proportional to the width of the sample. Quantitatively, the evolution of ξ(Ly) is expected to follow [101, 127]: ξ = (βLy + 2 − β)le. (5.10) le is the mean free path and β is the symmetry index. β = 1 corresponds to the Gaussian Orthogonal Ensemble universality class GOE while β = 2 for the Gaussian Unitary Ensemble GUE. Note that this change in β is accompanied by an artificial doubling of the number of propagating modes as a consequence of the breaking of Kramers degeneracy [101] and the modification of the definition of the quantum of conductance (equation (3.13)). In GUE, the quantum of conductance is then twice smaller than in GOE. Comparison of numerical localization lengths for different J with (5.10) is shown in fig 5.8. In this curve, the elastic mean free path is determined for J = 0 by fitting the numerical data with the previous expression for the localization length. In units of lattice spacing, this length is found equal to 60. For J 6= 0, we deduce the value of the elastic mean free path using the ratio: le(J)/le(0), which is found to be equal to the ratio of σ0(J)/σ0(0) (see section 5.3.2) using the Matthiesen rule. For the largest values (J = 0.2 and J = 0.4) of magnetic disorder, a comparison between the value found by this method and a fit using equation (5.10) gives very close results. Excellent agreement is found for J = 0 (GOE class, β = 1). In the case J 6= 0 we observe a crossover between GOE and GUE for intermediate values of magnetic disorder, while a good agreement with the GUE class is reached for J ≥ 0.2. The intermediate values of J are not compatible with the linear behavior (5.10) (see in particular the curve for J = 0.05). This signals a non-universal behavior of localization properties for intermediate magnetic disorder. From these results, we already notice that the localization regime is reached for much longer wires in the GUE case than for GOE. As shown below, this allows for an easier numerical  investigation of the universal metallic regime in the GUE case: magnetic impurities help in finding the universal conductance fluctuations! Theory, GOE Theory, GUE Figure 5.8: Evolution of localization length as a function of transverse length. le is the mean free path of the diffusive sample. Different behavior of the localization length if J = 0 (GOE) or J 6= 0 (GUE). Notice that for intermediate values of the magnetic disorder (for instance consider the case J = 0.05 of figure 5.8) the behavior of the localization length with the transverse length of the system is incompatible with the linear universal law. This regime of intermediate magnetic disorder amplitudes is the relevant experimental case. Up to my knowledge, this non universal behavior is not yet understood analytically. This regime is presently under investigation: the determination of the localization length for smaller values of the transverse length Ly and for smaller values of magnetic disorder J allows to conclude that for small Ly and J ≈ 0, ξ follows the J = 0 universal law, and that the slope of the linear behavior changes to the GUE case when Ly is increased. For moderate values of J (squares, diamonds), the law at large Ly seems to have the right slope but a different y-intercept. The accurate characterization of the localization length in both universal regimes opens the route for a study of the insulating regime on the one hand and of the metallic regime on the other hand. The next section deals with the study of universal properties in the localized regime.