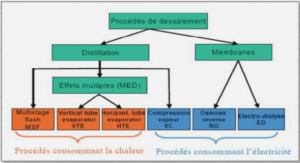
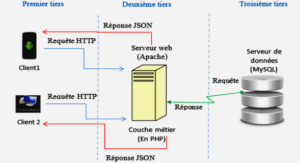
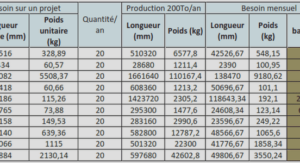
A topographically modified KdV approximation
In this chapter we discuss the validity of the previously derived uncoupled KdV approxi- mation on a large time scale for different bottom topographies. We demonstrate its validity for less restrictive bottoms, but provide two examples of simple bottoms for which the ap- proximation diverges. A new approximation that takes the bottom into account is finally derived. Starting from the previous theorem, it is worth wondering if this one holds for less restrictive initial data and bottoms, i.e. without any condition of a sufficient decay rate at infinity. In this view, we focus in a more general way on the last three terms of U This theorem proves that the approximation is less precise on a large time scale if we weaken the assumptions on the initial data and bottom, that is to say if we remove the assumption of a sufficient decay rate at infinity. And yet, it is worth pointing out that the regularity imposed on b in this theorem excludes many physical cases of interest. We focus from now on two simple examples of bottoms which do not fall into the scope of Theorem 5.1.1 : a regular step, and a slowly varying sinusoidal bottom. Our goal is to emphasize the fact that the approximation (v) in these two simple cases. A topographically modified KdV approximation which is still valid for such topographies is derived at the end of this chapter.In order to simplify the analysis, we only consider the approximation corresponding to a We mention that such a type of periodic bottom varying on a slow spatial scale has been studied in [21] by Craig-Guyenne-Nicholls-Sulem, with the difference that the authors authorized the bottom to vary also on a small spatial scale.
The reason of this choice is that we are interested in their physical meaning. Indeed, we further see – in Part III – that they are responsible for the reproduction of the phenomenon of shoaling. We hence decided to include these terms in the approximation. Remark 5.2.3. This modified version is quite interesting numerically since the topographi- cal terms are computed explicitly from the solution of the KdV equations. We thus expect the numerical simulation of this model to be faster than the one of the symmetric Boussinesq model (Σ). This point is checked in Part III. . Once more, we can propose a valid approximation just by including this term in the order one terms of the ansatz. We conclude this chapter with the proposition of a new approximation that remains valid in the periodic framework :