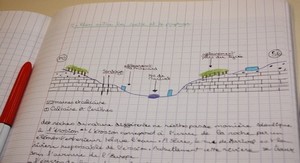
Les deux montages de laboratoire
Les optiques X de laboratoire ont connu des améliorations significatives ces 15 dernières années. Ces développements sont encouragés par les très nombreux utilisateurs des sources de laboratoire. Les optiques sont nombreuses et les deux configurations composées d’une optique d’entrée et d’une optique de sortie les plus utilisés lors de ce travail seront décrites. Le principe d’émission des rayons X en laboratoire sera brièvement rappelé.
Tube à Rayons X Les tubes à rayons X sont basés sur un principe simple : il s’agit de bombarder une anti-cathode avec un faisceau électronique accéléré par une haute tension électrique. Les électrons sont freinés par les atomes de la cible, ce qui provoque un rayonnement continu de freinage (Bremsstrahlung). Les électrons excitent également les atomes de la cible : ceux-ci réémettent alors un rayonnement X caractéristique par phénomène de fluorescence X. Le spectre sortant du tube est donc la superposition de ce rayonnement de freinage et de la fluorescence des différents éléments de la cible. Les deux diffractomètres du laboratoire sont montés avec un tube à cathode de cuivre, qui est la cathode la plus utilisée 3 . La plupart du temps, seule la raie d’émission Kα1 du cuivre est utilisée. Il s’agit de la radiation la plus intense du spectre. Elle est centrée autour de 1.5406Å soit une énergie de 8.048keV avec une largeur à mi-hauteur de 2.2eV . La raie Kα2 sensiblement deux fois moins intense est assez proche à 1.5444Å soit à 19.8eV de la Kα1.
Le tube utilisé posséde deux modes, le mode ponctuel et le mode linéaire. On passe de l’un à l’autre en le tournant d’un quart de tour. En mode linéaire la source est de 12mm × 400µm. En mode pontuel, la source est réduite à 1.2mm × 400µm compte-tenu de l’angle de take-off de 6◦ 4.
Optique hybride – Analyseur L’optique dite hybride est composé d’un miroir parabolique multicouche à pas variable suivi d’un monochromateur en Germanium 220 en géométrie 4 reflexions (channel cut). Le miroir multicouche permet à la fois de récupérer un maximum d’intensité du faisceau primaire tout en collimatant et préparant la monochromatisation. Les pas des empilements de la multicouche sont variables pour tenir compte de la variation de l’angle d’attaque du faisceau primaire sur le miroir (cf Diagramme de Dumond). Le monochromateur 4 réflexions améliore ensuite la sélection chromatique. Ce système permet finalement de sélectionner une portion de la raie Kα1 du cuivre avec une largeur d’environ 1eV . La raie Kα2 est donc filtrée. La combinaison de ces deux éléments permet également d’obtenir un faisceau très collimaté avec une divergence limitée seulement à 0.007◦ . Un système de fentes réglables manuellement compléte cette optique d’entrée. Il est possible en fermant au maximum ces fentes d’obtenir un faisceau de 20µm dans une direction. Ainsi, si l’échantillon s’y prête (bon pouvoir diffractant pour pallier au flux incident limité) des expériences de micro-diffraction sont possible en laboratoire ! La nature du faisceau obtenu avec cette optique fixe la manière dont on doit ajuster les pics de diffraction. Le faisceau est monochromatique, une simple pseudoVoigt a donc été utilisée comme fonction d’ajustement. La pseudo-Voigt est la somme d’une gaussienne et d’une lorentzienne centrées sur la même position et possédant la même largeur 5 . Le bruit de fond est ajusté par l’adjonction d’un polynôme.
Caratéristiques des dispositifs expérimentaux utilisés
Optique polycapillaire – Fentes longues Pour pallier à ces problèmes de flux, la configuration composé d’un polycapillaire en entrée est particulièrement complémentaire. Le polycapillaire est composé d’un grand nombre de fibres qui agissent comme guide d’onde permettant une collimation d’une large gamme énergétique. Le flux obtenu est alors tout à fait satisfaisant. Ainsi, elle est particulièrement efficace pour étudier les contraintes moyennes dans les films très minces (faible volume diffractant) par technique des sin2 (Ψ) et ceci même pour des pics d’indices élevés. Le flux est appréciable également pour les figures de pôle. Cependant la divergence est médiocre autour de 0.3◦ et la dispersion chromatique est importante. Elle laisse passer le doublet Kα et la Kβ. La présence de la Kβ ne pose pas de problème particulier car les angles de diffraction sont bien décalés même pour les réflexions de faibles indices 6 . Les fentes longues situées avant le détecteur permettent de sélectionner plus proprement les angles ~kf (moins efficacement qu’avec l’analyseur).
En revanche, il convient d’être prudent avec les 2 raies Kα. Cette caractéristique se voit bien aux grands angles avec un pic dédoublé (Fig 3.4b) mais aux faibles angles l’effet n’est pas visible à l’oeil (Fig 3.4a). Mais cet inconvénient peut être tourné en avantage. En effet avoir 2 radiations signifie faire la même mesure avec 2 énergies différentes. On peut alors comparer les résultats issus respectivement de la raie Kα1 et Kα2 si on est capable de séparer correctement les deux contributions. Dans la pratique, le problème revient au choix judicieux du modèle utilisé pour ajuster les courbes expérimentales. Plusieurs modèles ont été testés. Le plus stable est de travailler en déformation. La position des deux pics issus des deux Kα dépend en effet non seulement de l’indice hkl mais aussi de la déformation. En utilisant la 6 l’écart minimal entre les spectres de la Kα et de la Kβ est de 1 degré pour les pics (400)Kα2 et (420) 56 Chapitre 3. Réalisations expérimentales loi de Bragg, on obtient une relation entre les deux angles de diffraction et les deux énergies.
Avec cette approche, les deux contributions sont correctement extraites même pour des pics bas angles ou le dédoublement n’est pas évident (Fig 3.4a). Il est possible d’ajuster l’asymétrie des pics : il s’ agit de coder par morceaux la pseudo-Voigt qui posséde alors une largeur droite et une largeur gauche. Cependant avec ce modèle à deux raies, le modèle devient moins stable avec l’apparition d’artefacts. Ce raffinement est à reserver au modèle à une raie. Remarques Il faut toujours privilégier en laboratoire une configuration coplanaire pour travailler avec la plus faible divergence. Les pics asymétriques en géométrie ω sont donc à privilégier bien que pour des raisons de contrainte géométrique ils soient moins nombreux à pouvoir être mesurés (Fig. 4.6a).
Montages Synchrotron
Les expériences de diffraction ont été réalisées sur deux lignes notamment conçues pour faire de la diffraction cohérente : la ligne Cristal au synchrotron Soleil et la ligne ID01 à l’ESRF. Ces deux lignes ont des caractéristiques similaires (cf Fig. 3.5). Elles différent essentiellement par leur onduleur et leur optique finale. L’extension de la source primaire dépend de l’onduleur utilisé : sur ID01 elle mesure à mi-hauteur (full-width) environ 134 × 24 µm et 900 × 20 µm sur Cristal .
Energie Le rayonnement issu de l’onduleur est un faisceau polychromatique. Un monochromateur Si(111) en géométrie 2 cristaux est utilisé sur les deux lignes. L’un des deux miroirs est courbé pour assurer une focalisation sagitalle. L’énergie est souvent modifiée sur les lignes de lumiére et de légères dérives peuvent entrainer une erreur sur l’énergie affichée. Il faut donc calibrer l’énergie à chaque campagne de mesure. Une erreur de 10eV à 8.1keV sur une réflexion 111 de l’or donne une erreur de 0.12% sur la déformation : c’est énorme si une mesure absolue de celle-ci est recherchée !
Expérimentalement, l’énergie peut être calibrée avec une poudre de référence dont le paramétre de maille est exactement connu. Mais il est préférable d’avoir un analyseur en sortie. Lors des expériences réalisées, l’énergie a été calibrée en mesurant le seuil d’absorption de l’or. Ce seuil est parfaitement connu à E = 11.9187keV .
Préparation finale du faisceau
Aprés le monochromateur le faisceau est conditionné par les fentes secondaires F2 ou ss2. Ces fentes peuvent réduire la taille effective de la source primaire vue par l’échantillon. Le faisceau poursuit son chemin à travers les cabanes expérimentales en traversant un nombre limité de fenêtres. Un faisceau possédant une structure la moins génante possible est recherché. Dans l’idéal, un faisceau de ≃ 3 × 3µm en forme de porte est souhaitable, avec une amplitude parfaitement constante et un front d’onde parfaitement plan. Avec ce type de faisceau, le signal de diffraction collecté est uniquement l’image de la forme et de la déformation de l’objet étudié. Il ne dépend pas du faisceau incident. Bien sûr ce type de faisceau n’existe pas. Une configuration qui s’en rapproche le plus a été mise en place.
Le faisceau final qui atteint l’échantillon dépend de tous les éléments optiques présents entre la source et lui-même. Cependant la dernière optique joue un rôle prépondérant. Deux optiques finales différentes ont été utilisées. Sur Cristal, le faisceau est conditionné par des fentes placées le plus proche possible de l’échantillon. Sur ID01 des lentilles de béryllium ont été installées. Leurs influences sur le faisceau est discuté dans les deux prochains paragraphes. Remarque Le flux n’est pas vital dans le cas des grains étudiés. Ils sont volumineux ≃ 1 × 1 × 0.4 µm. L’or est dense. Le signal collecté est donc suffisant même en ne focalisant pas. En mode de comptage de photon unique (cf section 3.3.3 ), l’intégration du signal est négligeable par rapport au temps de lecture (read-out).Sur une des expériences, le flux était même trop important. Pour se placer en faible comptage, le temps d’intégration du signal peut être réduit. Mais celui-ci ne doit pas être réduit sous 0.1s pour éviter les problèmes de synchronisation entre l’obturateur (fast shutter ) et le temps de lecture de la caméra. Un problème de synchronisation peut être catastrophique faisant apparaître des trainées sur le signal caméra.
Lorsque le temps d’intégration limite est atteint et que l’intensité mesurée est toujours trop haute, la seule solution est de dérégler volontairement l’onduleur. L’utilisation d’atténuateurs est à proscrire lors d’une expérience de diffraction cohérente pour ne pas perturber le front d’onde. En revanche, un petit faisceau était essentiel pour localiser la zone d’intérêt de l’échantillon et le grain diffractant (cf §. 4.4).
ctives
Lors des expériences une fois le faisceau placé sur le grain choisi, la structure du faisceau a été caractérisée. Un grain de dimension sub-micronique a été utilisé pour évaluer la forme du faisceau projeté. Une carte (x,y) de l’intensité intégrée du pic 111 a été acquise en translatant l’échantillon avec les moteurs de translation. Cette carte est tracée figure 3.8b. Il s’agit de l’image de la convolution entre la forme du grain et la forme du faisceau. Cette convolution présente une tache centrale qui est sensiblement gaussienne de largeur à mi-hauteur (hx × hz) = 3.07 × 2.14µm. Le grain est donc illuminé de manière raisonnablement homogène. Sur cette carte, les rebonds de diffraction des fentes ss4 placées 25cm avant le système focalisant sont repérables. Ces rebonds sont assez loin de l’objet étudié (> 4µm). Il est raisonnable de considérer qu’ils n’ont aucun impact sur la mesure.
Les lentilles ont une mauvaise réputation en terme d’aberrations. La question des distorsions du front d’onde inhérente aux contraintes de leur fabrication sité, défauts de forme… ) est posée. Cependant dans l’approximation d’un faisceau gaussien, il a été montré 7 que la tache centrale de focalisation posséde un front d’onde raisonnablement plan [Schroer 2008]. Remarques Sur ID01 des lentilles diffractives de Fresnel sont également disponibles 8 . Elles permettent d’obtenir des faisceaux de l’ordre de 250 nm. Cette taille de faisceau est trop faible pour les grains étudiés. En revanche dans de polycristaux composés de grains plus petits ( < 200 nm), elles seraient avantageusement utilisables. Travailler avec des petits faisceaux et des petits objets reste néanmoins difficile. Les mesures sont particulièrement sensibles aux vibrations et aux dérives du montage expérimental qui est très complexe.
Cohérence des faisceaux utilisés
Caractériser la cohérence du faisceau est essentiel lors d’expériences de diffraction cohérente. Les grains doivent être illuminés avec un faisceau entièrement cohérent. Malheureusement le faisceau délivré par les sources synchrotrons n’est que partiellement cohérent. (cf §. 2.1). Les longueurs de cohérence doivent donc être supérieures aux dimensions des objets étudiés. Les longueurs de cohérence des différentes configurations expérimentales utilisées sont évaluées dans cette section.
Longueur de cohérence temporelle La longueur de cohérence longitudinale est
la plus simple à évaluer. Il suffit de connaître la dispersion énergétique du faiceau. Les dispersions énergétiques ∆E/E des deux monochromateurs ID01 et Cristal sont respectivement annoncées à 10−4 et 2.10−4 . Il s’agit dans les deux cas d’un montage en géométrie deux réflexions sur cristal Si 111. La focalisation sagitalle est effectuée sur le premier cristal sur la ligne Cristal et avec le second sur ID01. Entre 8keV et 12keV , la longueur longitudinale diminue de manière significative.
Les détecteurs
Les détecteurs ont un rôle essentiel. Les détecteurs utilisés lors des expériences seront décrits dans cette section.
Les détecteurs 1D
Au laboratoire, deux détecteurs ont été utilisés. Le plus classique est le détecteur proportionnel à gaz. Il est basé sur une mesure de courant. Les photons X ionisent le gaz créant des ions et des électrons. Ces charges sont collectées sur les bords du dispositif plongé dans un fort champ électrique. Il faut veiller à travailler hors saturation pour obtenir une réponse linéaire (< 150000 coups/s). Un detecteur type pixel est également disponible sur le diffractomètre X-Pert du laboratoire. Il est basé comme les caméras Medipix ou Xpad sur le concept selon lequel chaque pixel rempli les fonctions de compteur individuel de photons. La version du laboratoire est une version linéaire des caméras. Ce détecteur a une très bonne sensibilité et une très bonne dynamique (> 107 coups/s). Il est très utile pour réduire le temps de comptage lors de long cycles de mesures. Il a été possible grâce à ce détecteur de faire des cycles thermiques rapidement ( un week-end contre une bonne dizaine de jour avec un détecteur à gaz).