Nouveau cadre de modélisation de la capture d’interface et de l’ébullition pour le refroidissement industriel

Cahn–Hilliard as an interface capturing method

This chapter presents the framework of the interface capturing based on the phasefield method. It is the first step to simulating a liquid/vapor interaction within the quenching process. The origins of the phase-field method in the Cahn & Hilliard theory will first be investigated. The obtained governing equations will then be explained. In the next section, a study of some mathematical properties of these equations is proposed. To get a solver allowing the interface capturing, a full space and time discretization of these equations will be established. Then, some numerical properties of the discretized equations will be described. Finally, a series of numerical simulations will be performed to have a first glimpse of the solver’s abilities.

Cahn–Hilliard origins

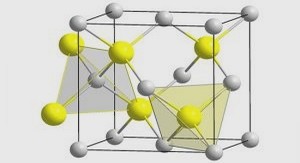
The origins of the Cahn–Hilliard equations come from phase transformations [1] and spinodal decomposition [2]. Phase transformations happen when a region in a material can decrease its free energy by modifying its structure, composition, or anything characterizing a phase within this material. These processes occur in many physical phenomena like melting, solidification, condensation, or evaporation for instance. Transformations from an unstable to a stable phase do not happen simultaneously within all the material but start in a part of the material due to spontaneous fluctuation in the material [3]. Spinodal decomposition is an example of phase transformation for which composition variations increase over time in a phase until two distinguished phases are created whose concentrations are determined by the equilibrium conditions. During this process, phases move from regions of low chemical potential to high chemical potential. That diffusion occurs to diminish the composition variations and to get a spatially uniform distribution of the chemical potential. The Cahn–Hilliard theory [4, 5] is based on a continuum equation for the kinetics of spinodal decomposition. In this theory, the free energy is a function of the concentration which has a spatial dependence. This concentration, called order parameter and denoted by φ, allows to identify two phases (Figure 1.1).  1 Cahn–Hilliard as an interface capturing method x φ 1 0 -1 Interface ε Phase 1 Phase 2 Figure 1.1: Order parameter identifying the phases It should be understood as being a volume fraction or a mass fraction. With the volume (or mass) fraction meaning, the order parameter is the volume (or mass) fraction per unit volume (or mass) of one phase, in a system having two phases. It takes the value +1 in the first phase and -1 in the second one with a thin, smooth transition region of width ε between the two phases (Figure 1.2). Consequently the interface in which these two phases coexist is described by the zero isocontour of the order parameter φ : Γt := {x ∈ Ω such that φ(x, t) = 0}, ∀t ∈ [0, tf ]. Figure 1.2: Two-phase system within the phase-field Cahn–Hilliard approach The free energy must increase if φ varies. Specifically, the free energy is minimized for a constant φ, therefore in the pure phases when φ = ±1. By considering the gradient of the order parameter as a measure of spatial variations in the concentration, the Ginzburg–Landau free energy functional [6] is defined as follows: E(φ) := Z Ω F(φ) + ε 2 2 |∇φ| 2 dx (1.1)

The governing equations where ϵ is the interface thickness and F is the homogeneous free energy.

This energy describes the entropy of mixing and takes into account the interaction between the two components. The second term of the integral is the energy used to form the interface separating the two phases. It penalizes large gradients and was introduced in the theory of phase transitions to model capillary effects. Some expressions for the free energy have been developed [4, 7–9]. One of the common expressions of the homogeneous free energy function is the quartic polynomial in the order parameter φ with a double-well potential form: F(φ) = 1 4 (φ 2 − 1)2 (1.2) for which two minima are reached for φ = −1 and φ = +1 corresponding to the two pure phases as represented in Figure 1.3. φ F(φ) φ = +1 φ = −1 Figure 1.3: Homogeneous free energy The double-well form is a fundamental physical assumption for the free energy F in the phase separation framework. A logarithmic expression of F can also be found in the literature [10–12]. However, because of its simplicity in the numerical framework, the usual form in the numerical literature is the polynomial expression (1.2). In the following, this expression of free energy is adopted, which is easier to work with. 1.3 The governing equations The Cahn–Hilliard equation can be derived from the total free energy functional which can be rewritten as E[φ] = F[φ] + G[φ] 25 1 Cahn–Hilliard as an interface capturing method where, F[φ] = Z Ω F(φ) dx and G[φ] = Z Ω ε 2 2 |∇φ| 2 dx In the following, boundary conditions on φ are assumed to be as follows: ∇φ · n = 0 on ∂Ω. Definition 1.3.1. Let φ be a real function, the directional derivative of a functional F[φ(x)] is defined by D[λ(x)]F[φ(x)] := lim µ→0 F[φ(x) + µλ(x)] − F[φ(x)] µ and is a linear functional of λ(x) and admits R α(x ′ )λ(x ′ )dx ′ as its representation, where α(x) := δF[φ(x)] δφ(x) = Z α(x ′ )δ(x ′ − x)dx ′ Definition 1.3.2. One defines the chemical potential ω as the first derivative of the free energy functional E with respect to the order parameter φ: ω := δE δφ Proposition 1.3.3. The chemical potential ω is related to the order parameter φ by the following relation: ω = −ε 2∆φ + F ′ (φ) (1.3) where F ′ (φ) = φ(φ 2 − 1). Proof. The directional derivative of E(φ) on ψ is D[ψ]E[φ] = Z Ω ψ δE[φ] δφ dx therefore δE[φ] δφ = δF[φ] δφ + δG[φ] δφ  Lemma 1.3.4. If F[φ] = Z f(φ(x))dx then, D[λ(x)]F[φ(x)] = Z λ(x) ∂ ∂φf(φ(x))dx whence δF[φ(x)] δφ(x) = ∂ ∂φf(φ(x)) By Lemma1.3.4, δF[φ] δφ = ∂ ∂φF(φ) = φ(φ 2 − 1) Let λ ∈ R and ψ ∈ H1 (Ω), then G[φ + λψ] = Z Ω ε 2 2 |∇(φ + λψ)| 2 dx = Z Ω ε 2 2 |∇φ + λ∇ψ| 2 dx = Z Ω ε 2 2 (|∇φ| 2 + 2λ∇φ · ∇ψ + λ 2 |∇ψ| 2 ) dx = Z Ω ε 2 2 |∇φ| 2 dx + Z Ω ε 2 2✁ 2✁λ∇φ · ∇ψ dx + Z Ω ε 2 2 λ 2 |∇ψ| 2 dx G[φ + λψ] = G[φ] + λε2   Z ∂Ω ψ ∇φ · n | {z } 0 dσ − Z Ω ψ∆φ dx   + λ 2 Z Ω ε 2 2 |∇ψ| 2 dx Therefore, G[φ + λψ] − G[φ] λ = − Z Ω ψ(ε 2∆φ) dx + λ Z Ω ε 2 2 |∇ψ| 2 dx Thus, D[ψ]G[φ] = lim λ→0 G[φ + λψ] − G[φ] λ = Z Ω ψ · (−ε 2∆φ | {z } δG[φ] δφ ) dx It comes that ω := δE[φ] δφ = φ(φ 2 − 1) − ε 2∆φ 27 1 Cahn–Hilliard as an interface capturing method Since the order parameter φ(x, t) must be conserved within the domain Ω in the absence of sources and sinks, this quantity satisfies to the continuity equation: dφ dt + ∇· J = 0 (1.4) where J representing the mass flux is determined by the Fick’s first law as J = −D∇φ (1.5) where D is the diffusion coefficient, which means that the mass flux points in the direction of decreasing concentration. Note that the usual uniform quantity in equilibrium is not the concentration φ but the chemical potential ω which is a thermodynamic quantity, unlike φ. A more general form of this driving force for diffusion is obtained by considering the chemical potential ω(x, t). For the i-th pure phase in the domain, Ji is induced by the gradient of the chemical potential: Ji = −cimi ωi ∂x (1.6) where ci and mi are respectively the concentration and the mobility of the i-th pure phase. Thus, the generalized statement of the Fick’s first law is given by: J = −M(φ)∇ω (1.7) where M(φ) is the mobility coefficient [13]. The diffusion within the system is always down the gradient of the chemical potential, i.e. from areas of high chemical potential to areas of low chemical potential. By combining this law with the continuity equation, it comes dφ dt + ∇· (−M(φ)∇ω) = 0. (1.8) With Equations (1.3) and (1.8), the Cahn–Hilliard equations are written as the following mixed formulation of a non-linear fourth-order diffusion equation for the order parameter φ: dφ dt − ∇· (M(φ)∇ω) = 0 (1.9) ω + ε 2∆φ − F ′ (φ) = 0 (1.10) Nowadays, this model is applied in diverse scientific fields, such as multiphase fluid flows, tumor growth, image processing, and population dynamics. 28 1.4. Mathematical properties In order to capture the interface and transport it with a flow velocity u in the fluid dynamics framework, the Cahn–Hilliard equations become: ∂φ ∂t + ∇· (φu) − ∇· (M(φ)∇ω) = 0 in Ω, (1.11) ω + ε 2∆φ − F ′ (φ) = 0 in Ω. (1.12) with the following initial and boundary conditions: φ(·, 0) = φ0 in Ω, (1.13) ∂φ ∂n = ∂ω ∂n = 0 on ∂Ω × [0, tf ]. (1.14) The degeneracy of the mobility M(φ) involves difficulties in the study of the Cahn– Hilliard equations. The mobility M(φ) = M is therefore assumed as constant and positive [14, 15]. However, in the literature [8, 16, 17], different forms of the mobility, constant or depending on φ, are suggested. Thus, the Cahn–Hilliard equations are equivalent to a convection-diffusion equation, with non-linear diffusion. The convection is given by the velocity field u which is assumed fixed, known, and with enough regularity (at least u ∈ C1 ), in all the present chapter. φ and ω are the two solution fields of these equations, which are consequently written under a mixed formulation. There is no exact solutions for d ≥ 2. Numerical methods must be used to determine the solutions and study their evolution. Before tackling the numerical framework, one introduces some mathematical properties of these equations.

Mathematical properties

The role of mathematics is to enable the theoretical and numerical validation of the models and approximations. Three components are in permanent interaction: 1. Modeling: to identify the phenomena to model, to identify the scales and the pertinent parameters for the phenomenon to model, to propose mechanisms explaining these phenomena, to propose simplified systems for which the mathematical study is possible, etc… 2. Theoretical analysis: proof of the ”well-posedness” characteristic of the models (existence and uniqueness of solutions), asymptotic analysis of the models (when the parameters tend toward zero), stability analysis of the stationary solutions (equilibrium points of the system), compactness study, etc… 3. Numerical analysis: proof of results justifying the relevance of the numerical approximation, effective calculation of the models approximated solutions,Cahn–Hilliard as an interface capturing method predicting the unstable behaviors, parameter dependency analysis, developing more robust and faster codes based on the mathematical analysis of the system, etc… In all the theoretical results introduced in the present chapter, the order parameter φ is assumed respecting the maximum principle. One notes that it is a strong hypothesis since it is the biggest difficulty in the mathematical analysis of the Cahn–Hilliard equations [18] The present section will focus on a brief review of the mathematical results of the model (1.11)-(1.14) introduced previously. These governing equations describe the time-space evolution of the macroscopic quantities involved in the mixture composition, i.e. the order parameter φ and the chemical potential ω. The Equations (1.11)-(1.12) associated to the boundary conditions (1.13)-(1.14) verify the following property, also called mass conservation of the Cahn–Hilliard equations.