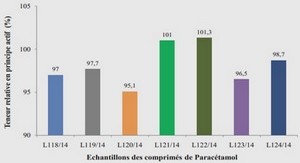
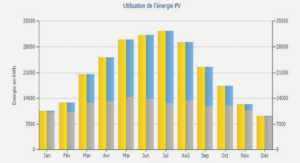
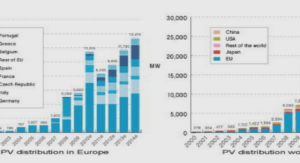
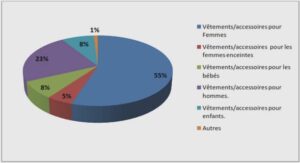
Solutions périodiques de quelques classes
des équations différentielles ordinaires

 Solutions périodiques et cycles limites 

Solutions périodiques

On appelle solution périodique toute solution x = ϕ(t) de l’équation ( 1.2.a), telle qu’il existe un nombre T > 0 vérifiant ϕ(t + T ) = ϕ(t). 16 1.10. SOLUTIONS PÉRIODIQUES ET CYCLES LIMITES Remarque 1.4 • Si ϕ(t) a une période T , la solution a aussi une période kT , et supposons que T est la plus petite période. • Les points d’équilibres sont considérés comme des solutions périodiques à une période arbitraire T ∈ R+ . Théorème 1.6 Soit ϕ(t) une solution du système ( 1.2.a), supposons qu’il existe deux instants t1 et t2 (t1 < t2 ) tels que ϕ(t1 ) = ϕ(t2 ) (c’est à dire que l’orbite de ϕ(t) se recoupe). Alors, ϕ(t) est une solution périodique définie pour tout t ∈ R. Lemme 1.1 Une solution périodique du système différentiel autonome ( 1.2.a) correspond à une orbite fermée dans le plan de phase, et une orbite fermée correspond à une solution périodique. 1.10.2 La méthode du gradient Définition 1.12 Supposons que le système différentiel puisse s’écrire sous la forme x˙ = − −−−−−−−−−→ gradV (x) où −−−−−−−−−−→ gradV (x) = ∂V ∂x1 ,….., ∂V ∂xn !T , et x ∈ U ⊆ Rn et V est une fonction de classe C 1 définie sur U à valeur dans R. On dit alors que V est un potentiel du système. Théorème 1.7 Si un système admet un potentiel il ne peut admettre d’orbites fermées. Exemple 1.3 Considérons le système ( x˙ = sin(y), y˙ = x cos(y), ce système n’admet pas d’orbites fermées puisqu’il admet la fonction V (x,y) = −x sin(y) comme potentiel. 1.10.3 Cycles limites Définition 1.13 On appelle cycle limite une orbite périodique qui est isolée dans l’ensemble des orbites périodiques, c’est à dire qu’on ne peut pas trouver une autre orbite fermée dans son voisinage. Définition 1.14 L’amplitude d’un cycle limite est la valeur maximale de la variable x du cycle limite.

SOLUTIONS PÉRIODIQUES ET CYCLES LIMITES

Stabilité des cycles limites

Théorème 1.8 Γ étant la trajectoire d’un cycle limite, toutes les trajectoires intérieures et extérieures voisines de Γ s’enroulent toutes en spirales autour de Γ pour t → +∞ ou t → −∞. 1. Le cycle limite est dit stable, si toutes les trajectoires intérieures et extérieures voisines sont attirées vers Γ. 2. Le cycle limite est dit instable, si toutes les trajectoires intérieures et extérieures voisines sont refoulées de Γ. Exemple 1.4 Soit le système différentiel    x˙ = x − y − x  x 2 + y 2  , y˙ = x + y − y  x 2 + y 2  . (1.10.a) En coordonnées polaires x = r cos(θ), y = r sin(θ) avec r > 0, le système ( 1.10.a) devient ( r˙ = r(1 − r 2 ), θ˙ = 1, d’où r˙ = 0 ⇒ r = 0 ou r = ±1. Comme r > 0, on n’accepte que la racine positive r = 1. Donc, pour r = 1 on a la solution périodique (x(t),y(t)) = (cos(t + θ0 ), sin(t + θ0 )), avec θ(0) = θ0 . Dans le plan de phase il y a un seul cycle limite d’équation x 2 + y 2 = 1 et d’amplitude r = 1. Figure 1.11 – Cycle limite du systme ( 1.10.a). 

EXISTENCE ET NON-EXISTENCE DES CYCLES LIMITES 

 Existence et unicité des cycles limites

Théorème 1.9 (Poincaré-Bendixson). On considère le système autonome ( x˙ = f (x,y), y˙ = g(x,y), (1.11.a) dans un domaine D ⊂ R2 , où f ,g ∈ C 1 (D). Supposons que γ + est une orbite bornée et positive et que ω(γ + ) ne contient que des points critiques. Alors ω(γ + ) une orbite périodique. De plus si ω(γ + ) , γ + alors l’orbite périodique est appelé cycle limite . Un résultat analogue est valable pour une orbite bornée et négative. Corollaire 1.10 Soit D un ensemble fermé borné ne contenant aucun point singulier et supposons que D est positivement invariant. Alors il existe un cycle limite contenu dans D. Théorème 1.11 (Critère de Dulac). On considère le système ( 1.11.a), où f et g sont de classe C 1 sur un ouvert E ⊂ Rn . Soit ψ une fonction de classe C 1 et A une région annulaire de E. Si ∂ ∂x (ψf ) + ∂ ∂y (ψg) ne change pas de signe dans A, alors il y a un seul cycle limite contenu dans A. 1.11.2 Non existence des cycles limites Théorème 1.12 (Critère de Bendixson). Supposons que le domaine D ⊂ R2 soit simplement connexe, f et g sont continûment différentiables dans D. Le système ( 1.11.a) n’admet pas de cycle limite dans D, si ∇(f ,g) non nulle et ne change pas de signe en D. Théorème 1.13 (Critère de Dulac). On considère le système ( 1.11.a) où f et g sont de classe C 1 . Soit ψ une fonction de classe C 1 . Supposons que le domaine D ⊂ R2 soit simplement connexe. Si ∂ ∂x (ψf ) + ∂ ∂y (ψg) non nulle et de signe constant sur D, alors il n’y a pas de cycle limite contenu entièrement dans D. 1.11.3 Intégrales premières On dit qu’une fonction H : Ω ⊂ R2 → R de classe C 1 est une intégrale première du système ( 1.11.a) si elle est constante sur les courbes solutions (x(t),y(t)) de ce système, c’est-à-dire dH(x,y) dt = ∂H (x,y) ∂x f (x,y) + ∂H (x,y) ∂y g(x,y) ≡ 0, sur les points de Ω. On dit que le système différentiel ( 1.11.a) est intégrable sur un ouvert Ω, s’il admet une intégrale première sur Ω.

BIFURCATION DE HOPF 

Théorème 1.14 Soit le système planaire ( x˙ = fµ (x,y), y˙ = gµ (x,y), (1.12.a) où µ est un paramètre. Supposons que (x,y) = (x0 ,y0 ) est un point d’équilibre du système ( 1.12.a) qui dépend de µ. Soient λ1,2 (µ) = α(µ) ± iβ (µ) les valeurs propres du système linéarisé au voisinage de (x0 ,y0 ). Supposons que pour une certaine valeur de µ = µ0 , les conditions suivantes sont satisfaites 1) α(µ0 ) = 0, β (µ0 ) = w , 0 où sgn(w) = sgn ∂gµ ∂x   µ=µ0 (x0 ,y0 )  , 2) dα(µ) dµ   µ=µ0 = d , 0, 3) a , 0 où a = 1 16  fxxx + fxyy + gxxy + gyyy + 1 16w (fxy  fxx + fyy −gxy  gxx + gxy −fxxgxx +fyygyy), avec fxy = ∂ 2 f ∂x∂y   µ=µ0 (x0 ,y0 ). Alors une orbite périodique bifurque du point d’équilibre pour µ > µ0 si ad < 0 ou pour µ < µ0 si ad > 0. Le point d’équilibre (x0 ,y0 ) est stable pour µ > µ0 (respectivement pour µ < µ0 ) si d < 0 (respectivement si d > 0). L’orbite périodique est stable (respectivement instable) si le point d’équilibre est instable (respectivement stable). L’amplitude de l’orbite périodique est égale à q  µ − µ0    et la période est de T = 2π |ω| quand µ → µ0 . La bifurcation est dite super-critique si l’orbite périodique est stable et sous-critique si l’orbite périodique est instable. Exemple 1.5 On considère le système non linéaire suivant ( x˙ = y + x(µ − x 2 − y 2 ), y˙ = −x + y(µ − x 2 − y 2 ), (1.12.b) le système ( 1.12.b) admet un point d’équilibre unique qui est l’origine (0,0). Les valeurs propres de la matrice Jacobienne calculées au point d’équilibre (0,0) sont complexes conjuguées et égales à λ1,2 = µ ± i . Alors α(µ) = µ et β (µ) = 1. On a α(µ) = 0 ⇐⇒ µ0 = 0, sgn(ω) = sgn[−1], β(µ0 ) = −1 = ω , 0, ∂α ∂µ   µ0=0 = 1 = d , 0 et a = −1. 20 1.12. BIFURCATION DE HOPF Donc on a une bifurcation de Hopf et la valeur de la bifurcation est µ0 = 0. D’après le Théorème (1.14), on a ad = −1 < 0, donc il existe un cycle limite pour µ > 0. Comme d = 1 > 0, l’origine est stable pour µ < 0 et instable pour µ > 0. Pour µ > 0 le cycle limite est stable d’amplitude √ µ. On dit alors qu’on a une bifurcation de Hopf super-critique .