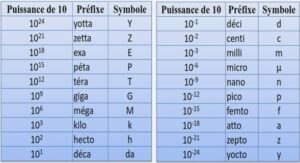
Expression hyperdéterminantale des coefficients dans le développement de ∆ sur les fonctions de Schur

Hyperdéterminants de Hankel

Les hyperdéterminants sont des objets inventés par Cayley en 1843. Ils regroupent plusieurs généralisations du déterminant pour les hypermatrices de plus de deux indices. L’hyperdéterminant que nous utilisons dans ce chapitre est le plus simple des hyperdéterminants car il généralise de façon naturelle les formules des déterminants considérés comme des sommes multi-alternées : 

Hyperdéterminants et intégrales 

Soit M = (Mi1,…,ip )1≤i1,…,ip≤n un tenseur à p indices, l’hyperdéterminant de M est la somme alternée sur les p copies du groupe symétrique Sn, Det(M) := 1 n! X σ1,…,σp∈Sn sign(σ1 … σp) Yn i=1 Mσ1(i)…σp(i) . (26) Si p = 2, on retrouve la définition des déterminants. Par exemple, si p = 4 et n = 2, Det(M) = −M2,1,1,1M1,2,2,2 + M2,1,1,2M1,2,2,1 + M2,1,2,1M1,2,1,2 − M2,1,2,2M1,2,1,1 + M2,2,1,1M1,1,2,2 − M2,2,1,2M1,1,2,1 − M2,2,2,1M1,1,1,2 + M2,2,2,2M1,1,1,1. Remarque : l’hyperdéterminant Det est nul lorsque p est impair. Dans la suite du chapitre, on supposera que p = 2k est pair. Nous allons analyser le cas particulier de l’hyperdéterminant de Hankel. Il s’agit d’un hyperdéterminant dont les entrées dépendent seulement de la somme des indices. Cet hyperdéterminant s’écrit : H f := (f(i1 + · · · + i2k))0≤i1,…,i2k≤n−1. (27) Plus généralement, on définit l’hyperdéterminant de Hankel décalé par des vecteurs décroissants λ (1),… ,λ(2k) ∈ Z n comme l’hyperdéterminant du tenseur de Hankel décalé H f λ(1),…,λ(2k) := (f(λ (1) i1 + · · · + λ (2k) i2k + i1 + · · · + i2k))0≤i1,…,i2k≤n−1. (28) 10.2 Hyperdéterminants et intégrales Certains hyperdéterminants peuvent être obtenus à l’aide d’intégrales multiples de produits de déterminants.

Proposition 10.2.1.

(Identité de Heine généralisée) Soit (f (i) j ) 1≤i≤2k 1≤j≤n une famille de fonctions et µ une mesure sur C telle que les intégrales apparaissant dans l’équation (29) soient définies. Alors, on a 1 n! Z … Z det(f (1) j (zi))… det(f (2k) j (zi))dµ(z1)… dµ(zn) = Det Z f (1) i1 (z)… f(2k) i2k (z)dµ(z)  1≤i1,…,i2k≤n . (29) Démonstration. Le résultat s’obtient en développant les termes situés de part et d’autre de l’égalité (29). Remarque : ici, seule la linéarité de l’opération R dµ(z) intervient. L’intégrale peut donc être remplacée par n’importe quel opérateur linéaire. Si nous appliquons la proposition 10.2.1 au produit d’une fonction de Schur et d’une puissance du discriminant, nous obtenons un hyperdéterminant de Hankel décalé dont les entrées sont des sommes associées à la mesure µ. 

Corollaire 10.2.2.

Soit µ une mesure sur C telle que l’intégrale apparaissant dans l’équation (30) soit définie, on a 1 n! Z … Z Sλ(z1,… ,zn)∆2k dµ(z1)… dµ(zn) = Det(cλn−i1+1+i1+···+i2k−2k) (30) où cn = R z ndµ(z). Démonstration. Il suffit de remarquer que Sλ(z1,… ,zn)∆2k = det(z λn−j+1+j−1 i ) det(z j−1 i ) 2k−1 et d’appliquer (29). 10.3 Algorithme pour obtenir les coefficients Dans la section précédente, nous avons vu que ( équation 30 ) 1 n! Z … Z Sλ(z1,… ,zn)∆2k dµ(z1)… dµ(zn) = Det(cλn−i1+1+i1+···+i2k−2k). (31) Cette formule nous donne une expression hyperdéterminantale des coefficients g n,k λ décrite dans le corollaire 10.3.1. Soit λ (1),… ,λ(2k) 2k vecteurs décroissants de Z n . Nous définissons le tenseur à 2k indices ∆λ(1),…,λ(2k) :=  δ λ (1) n−i1+1+···+λ (2k) n−i2k+1+i1+···+i2k,(2k−1)n+1 1≤i1,…,i2k≤n et Dλ(1),…,λ(2k) := Det