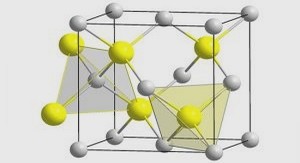
Shape memory alloys (SMAs) have been the focus of extensive research in the past few decades. The unique properties of SMAs have made them a suitable choice in a wide variety of industries, including aerospace, automotive, robotics, oil and gas, surgical instruments and biomedical implants (Jani, Leary et al. 2014). These materials exhibit two main behaviors: shape memory effect (SME) and superelasticity (SE), also known as pseudoelasticity. SME is observed when the material recovers its original shape by heating above a certain temperature, after initially being deformed at a lower temperature. SE refers to the ability of these materials to undergo large reversible deformation at a constant temperature. The magnitude of superelastic strains can reach 11% (Duerig, Pelton et al. 1999), which is significantly higher than the elastic deformation of conventional metals such as steel, for which a strain of approximately 0.1% is usually considered reversible. These two characteristics both stem from the crystallographic structure of the material and a process known as martensitic transformation (MT), a diffusionless phase transformation between two crystallographic states of austenite and martensite. The austenite (or parent) phase has a cubic crystal structure, and is stable at higher temperatures, while the martensite phase has a monoclinic crystal structure, and is stable at lower temperatures. The MT can be induced by both temperature variation and stress. The martensite phase can have multiple variants, theoretically 24 of them, marked by austenite-martensite interface planes known as habit planes. In absence of stress, different variants of martensite form a self-accommodating twinned arrangement. In case of stressinduced MT, however, martensite becomes de-twinned under the stress, i.e. it reorients into different combinations of favorable variants, in order to accommodate the applied strain (Otsuka and Wayman 1999, Popov and Lagoudas 2007). This leads to large macroscopic deformation. If the material is heated above a certain temperature, the martensite transforms into austenite, recovering the deformation; this constitutes SME. However, if the material is in austenite phase, it can directly transform to de-twinned martensite phase under stress and transform back to austenite upon unloading, hence, exhibiting pseudoelastic behavior.

Another feature of some SMAs is their ability to exhibit two-way shape memory effect (TWSME) which, unlike other SMA behaviors, is not and inherent property of the SMA, and is rather acquired through applying special loading cycles or training in a certain temperature range in order to accumulate unrecovered strains in the material. A trained SMA is able to undergo two-way transformations between martensite and austenite, when subjected to temperature changes, hence generating macroscopic strains, without the need for mechanical loading (Cisse, Zaki et al. 2016).

Several types of alloys exhibit shape memory properties, including Nickel-Titanium (NiTi or Nitinol), iron-based alloys, such as Fe–Mn–Si, and copper-based alloys, such as Cu Zn–Al. Despite their relatively higher cost, NiTi SMAs are the favorite choice in most applications due to their superior thermo-mechanical performance and stability (Wilkes and Liaw 2000, Huang 2002).

SMAs in porous form can offer several benefits that originate from both porosity and SMA characteristics. Metallic foams, in general, have found many applications in a variety of applications and industries, including biomedicine, aerospace, military, transportation, construction, etc. (Bansiddhi, Sargeant et al. 2008, Bram, Köhl et al. 2011, Smith, Guan et al. 2013). Porous structures can provide many advantages, such as high stiffness to weight ratio, vibration damping, shock absorption and light weight that make them an attractive material choice (Gibson and Ashby 1999, Deshpande and Fleck 2000, K.R. Mangipudi 2010).

One example of the applications where the porous SMAs have attracted a lot of attention is the field of bone implants. A crucial factor in designing a bone implant is its chemical and mechanical biocompatibility. NiTi alloys are usually chosen for biomedical applications because of their chemical biocompatibility on par with titanium and stainless steel (Ryhänen, Kallioinen et al. 1998, Thierry, Merhi et al. 2002). There are some concerns regarding the nickel content of this alloy, as it can leach into the body and cause health problems, but many methods have been proposed to prevent the nickel release, such as different surface treatments. Also, because of the strong intermetallic bond between titanium and nickel, the leaching is minimal and mainly limited to corrosion (Bansiddhi, Sargeant et al. 2008).

Modeling of Porous Metals 

In the literature, modeling of porous structures is usually performed on two different scales: mesoscale and macroscale . On mesoscale, the porous substructure is studied, and one or more cells inside a small volume known as representative volume element (RVE) are analyzed. Once the mechanical behavior of this volume is determined, the volume can be treated as a non-porous medium that represents the behavior of porous material. The majority of the proposed modeling methods to simulate porous structures’ behaviors are developed on mesoscale and utilize the concept of RVEs. In models developed on macroscale, however, the whole porous structure is analyzed.

Based on the substructure arrangement, the porous materials can be divided into two groups of random and ordered substructures, which is also a distinct characteristic in categorizing the modeling approaches. The ordered or regular porous structures consist of identical substructure units or cells which are repeated throughout the structure. However, in a random porous structure, the underlying cells vary in size and geometry across the domain.

Analytical modeling of RVEs 

The main advantage of analytical methods for determining the mechanical behavior of porous material is the low computational costs. However, a certain amount of simplification is usually necessary to achieve a model that can be handled analytically. This method can be used for both random and ordered structures.

Analytical modeling of random structures 

In order to model random porous microstructures analytically, it is usually necessary to apply some sort of simplification. In the most simplified approach, a random cellular material can be assumed to be ordered. Janus-Michalska and Pęcherski worked on modeling of open cell foams and used a simplified unit cell in periodic setting. Each unit cell was a tetrahedron containing four beams. Using analytical methods, they formulated the mechanical characteristics of theunit cell based on beam theory and eventually developed relations for the effective behavior of the foam in macro-scale. The key concept of their work was making use of the Kelvin moduli obtained from the unit cell elasticity tensor as a common parameter relating the micro and macro formulations (Janus-Michalska and Pęcherski 2003). Reyes, Hopperstad et al. used an existing constitutive model and applied statistical density variation to model the heterogeneous mass distribution in aluminum foam, and included fracture criteria implemented in a series of FE analyses to validate their model (Reyes, Hopperstad et al. 2003).

Another group of analytical models for random porous materials make use of averaging techniques. Qidwai, Entchev et al. worked on modeling of porous SMAs using micromechanical averaging based on the Mori-Tanaka stress averaging method (Mori and Tanaka 1973) where a random porous structure was treated as a composite material with pores as inclusions (Qidwai, Entchev et al. 2001). Entchev and Lagoudas also did a similar study on porous shape memory alloys with random pore distribution using the Mori-Tanaka averaging method for estimation of the overall stiffness properties (Entchev and Lagoudas 2002, Entchev and Lagoudas 2004). In another work, Zhao and Taya accounted for the pores as inclusions based on Eshelby’s equivalent inclusion method and Mori-Tanaka averaging method (Eshelby 1957, Mori and Tanaka 1973) and formulated relations for the macroscopic behavior (Zhao and Taya 2007). Nemat-Nasser, Su et al. used multi-phase composite model (MPCM) where a porous SMA is treated as a composite with two inclusions, martensite and austenite states, each being either matrix or inclusion, and the pores being the second inclusion (Nemat-Nasser, Su et al. 2005).