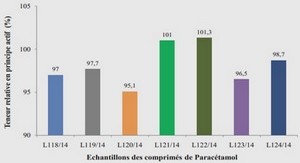
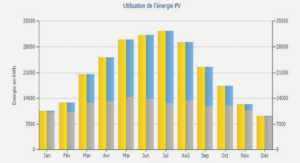
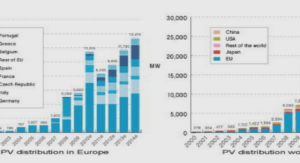
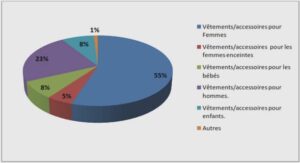
SIMULATIONS STOCHASTIQUES DANS LES METHODES DE KRIGEAGE

Géostatistique

Soit S un ensemble spatial, S ⊂ R 2 ou S ⊂ R 3 . Un champ aléatoire X sur S et à valeurs dans E est la donnée d’une collection X = {Xs, s ∈ S} de variables aléatoires (v.a) indexées par S et à valeurs dans E. Ce chapitre est consacré à l’étude des champs du second ordre, c’est-à-dire des champs à valeurs réelles (E = R) de variance finie en tout site s ∈ S. On étudiera également la classe plus générale des champs à accroissements stationnaires au second ordre ou modèle intrinsèque. L’approche géostatistique modèlise X par sa covariance (modèle au second ordre) ou par son variogramme (modèle intrinsèque). Développée initialement pour la modélisation et la prévision des réserves minières, la géostatistique est utilisée aujourd’hui dans des domaines très variés tels que les sciences de la terre, l’environnement, l’épidémiologie. 6 1.1 Quelques rappels Un processus aléatoire réel X = {Xs, s ∈ S} est une fonction mesurable X : S −→ R à valeur réelle. La loi du processus est caractérisée par ses lois jointes finies dimensionnelles (Xs1 , Xs2 , …, Xsn ) pour toute partie finie {s1, s2, …, sn} de S. Définition 1.1.1. X est un processus au second ordre (on note X ∈ L 2 ) si pour tout s ∈ S, E(X2 s ) < ∞. La moyenne est la fonction m : S −→ R définie par m(s) = E(Xs), la covariance la fonction c : S × S −→ R définie par c(s, t) = Cov(Xs, Xt). X est centré si m(s) = 0 en tout s. La propriété caractéristique d’une covariance est d’être semi-définie positive (s.d.p.) : ∀m ≥ 1, a ∈ R m et {s1, s2, …, sm} ⊆ S ; X i,j=1,m aiaj c(si , sj ) ≥ 0. Cette positivité résulte de l’égalité : V ar X i=1,m aiXsi  = X i,j=1,m aiaj c(si , sj ). La covariance est définie positive (d.p.) si de plus X i,j=1,m aiaj c(si , sj ) > 0 pour a 6= 0. Les processus gaussiens consituent une sous-classe importante des processus de L 2 . Définition 1.1.2. X est un processus gaussien sur S si, pour toute partie finie Λ ⊂ S et toute suite réelle a = (as, s ∈ Λ), X s∈Λ asXs est une variable gaussienne. 7 Si la covariance ΣΛ de XΛ = (Xs, s ∈ Λ) est inversible, XΛ admet pour densité : fΛ(xΛ) = (2π) −#(Λ)/2 (detΣΛ) −1/2 exp{−1 2 t (xΛ − mΛ) Γ−1 Λ (xΛ − mΛ)}. Ici, #(U) dénote le cardinal de U et mΛ = E(XΛ). A toute moyenne m et covariance c.d.p. est associé un unique champ gaussien de moyenne m et de covariance c. Exemple 1.1.3. Mouvement brownien sur R + ; convolution discrète et continue. (a) X est un mouvement brownien sur S = R + : Xo = 0, Xs ∼ N (0, s), s > 0 et les accroissements X([s, t]) = Xt − Xs, t > S ≥ 0 sont indépendants pour des intervalles disjoints. La covariance de X vaut : c(s, t) = min{s, t}. (b) S = Z 2 , c = (c(s, t),(s, t) ∈ S) est une suite réelle ne comportant qu’un nombre fini de termes non-nuls. Si ε est une suite de variables de L 2 la convolution discrète suivante définit un processus de L 2 dit en moyenne mobile : Xs,t = X S c(s − u, t − v)εu,v. (c) La version continue est la suivante : soit W un processus de Weiner sur R 2 (les accroissements W du, dv) sont gaussiens, centrés, indépendants, de variance du × dv). Si c : R 2 −→ R est une fontion de carré intégrable (σ 2 = Z R2 c 2 (u, v)dudv < ∞), l’intégrale suivante définit un processus gaussien (stationnaire) de variance σ 2 : Xs,t = Z R2 g(s − u, t − v) W(du, dv). 8 1.2 Processus stationnaire, covariance Soit X un champ sur S ⊂ R d de moyenne m et de covariance c où S est un sous-groupe additif de R d (par exemple S = R d ou S = Z d ). 

Définitions, exemples

Définition 1.2.1. X est un champ stationnaire au second ordre sur S si X est de moyenne constante et de covariance invariante par tanslation : ∀s, t ∈ S : E(Xs) = m et c(s, t) = Cov(Xs, Xt) = C(t − s). où C() est la fonction de covariance stationnaire. L’invariance par translation se traduit par : ∀s, t, h ∈ S : Cov(Xs+h, Xt+h) = C(s − t). La fonction de corrélation : ρ() est h 7−→ ρ(h) = C(h)/C(0). Proposition 1.2.2. : (1) ∀h ∈ S, |C(h)| ≤ C(0) = V ar(Xs) = σ 2 X. (2) ∀n ≥ 1, a ∈ Rn et {t1, t2, …, tm} ⊆ S : X i,j=1,m aiajC(ti − tj ) ≥ 0. (3) Si C1, C2 sont des covariances stationnaires, les fonctions suivantes le sont aussi : i) C(h) = a1C1(h) + a2C2(h), a1 et a2 ≥ 0 ; ii) C(h) = C1(ah), a > 0 ; iii) C(h) = C1(h) C2(h). Deux notions encadrent la notion de stationnarité dans L 2 : l’une, plus faible, étudiée au §1.3, est celle de processus à accroissements stationnaires 9 ou modèle intrinsèque ; l’autre, plus forte, est la stationnarité au sens strict : X est strictement stationnaire si pour tout k ∈ N, (t1, t2, …, tk) ∈ S k et ∀h ∈ S, la loi de (Xt1+h, Xt2+h, …, Xtk+h) ne dépend pas de h. Si X est stationnaire au sens strict et si X ∈ L 2 , alorfs X est stationnaire de L 2 . L’inverse n’est pas vrai en général, mais les deux notions coïncident si X est gaussien. Exemple 1.2.3. Bruit Blanc Fort (BBF), BB faible (BBf ), BB gaussien (BBG) X est un Bruit Blanc Fort si les v.a. {Xs, s ∈ S} sont centrées indépendantes et identiquement distribuées (i.i.d.). X est un Bruit Blanc faible si les variables {Xs, s ∈ S} sont centrées, V ar(Xs) = σ 2 < ∞, décorrélées : ∀s 6= t : Cov(Xs, Xt) = 0. Un BBF sur S est strictement stationnaire ; un BBf sur S est stationnaire de L 2 . X est un BB Gaussient si les v.a. {Xs, s ∈ S} sont i.i.d. gaussiennes centrées. Le champ X est isotropique si la covariance entre Xs et Xt ne dépend que de la distance euclidienne ks − tk entre s et t : un champ isotropique est stationnaire ; de plus : pour tout t, s ∈ S : C(s − t) = r(ks − tk). avec r la fonction de covariance isotropique. L’isotropie impose des restrictions sur la covariance si d ≥ 2. Par exemple, si X est centré isotropique sur R d , et si on considère (d+1) points à distance mutuelles h, E  X i=1,d+1 X 2 si  = (d + 1)[r(0) + dr(h)]. 10 On en déduit pour la corrélation ; pour tout h, ρ(h) ≥ −1/d, ρ(h) ≥ −0, 5 si d = 2 établit des minorations plus finies : ρ(h) ≥ −0.403 sur R 2 et ρ(h) ≥ −0.218 sur R 3 . 

Processus intrinsèque, variogramme

La stationnarité dans L 2 n’est pas toujours satisfaite : par exemple si Xs = Ys + Z où Y est stationnaire de L 2 mais Z /∈ L 2 ; ou encore si X ∈ L 2 n’est pas stationnaire (i.e. le mouvement brownien). Une façon d’affaiblir l’hypothèse de stationnaire L 2 est de considérer le processus : I (h) = {I (h) s = Xs+h − Xs, s ∈ S}, des h-accroissements de X, à h fixé, ces accroissements pouvant être stationnaires en s dans L 2 sans que X le soit ou que X ait une variance finie. Définition 1.3.1. X est un processus intrinsèque si X est de moyenne constante et si pour tout h ∈ S, le processus I (h) = {I (h) s = Xs−Xs+h : s ∈ S} est stationnaire au second ordre. Le variogramme de X est alors défini par : 2γ(h) = V ar(Xs+h − Xs) 2 γ() est le semi-variogramme de X. Par exemple, le mouvement brownien sur R est intrinsèque, non-stationnaire, de variogramme |h| non borné. Remarquons que tout processus stationnaire au second ordre est intrinsèque. On a : 11 Proposition 1.3.2. 1. 2γ(h) = 2γ(−h), 2γ(h) ≥ 0 et 2γ(0) = 0. 2. Un variogramme est condittionnelle défini négatif (c.d.n) : ∀a ∈ R n t.q X i=1,n ai = 0 et {s1, …, sn} ⊆ S : X i,j=1,n aiajγ(si − sj ) ≤ 0. 3. Si γ est borné au voisinage de 0, ∃a et b ≥ 0 tel que, pour tout x, 2γ(x) ≤ a||x||2 + b. Un variogramme 2γ() n’est pas nécessairement borné (considérer |h| pour le mouvement brownien) mais croît au plus comme ||h||2 . Un exemple de croissance quadratique γ(t) = σ 2 1 t 2 est celle du variogramme Xt = Zo + tZ1, t ∈ R, où Zo et Z1 sont centrées, indépendantes, 0 < σ2 1 = V ar(Z1) < ∞. Variogramme d’un processus stationnaire Si X est stationnaire de covariance C, X est intrinsèque de variogramme 2γ(h) = 2(C(0) − C(h)) (1.1) Il suffit de considérer le mouvement brownien pour voir que la réciproque est fausse. Cependant, si le variogramme de X est borné, alors Xt = Zt + Y pour un processus Z stationnaire de L 2 (Matheron, [34]). Si C(h) −→ 0 lorsque ||h|| −→ ∞, le semi – variogramme γ(h) présentera un palier au niveau C(0) = V ar(X) pour h −→ ∞. La portée du variogramme (resp. la portée pratique) est la distance à partir de laquelle le variogramme atteint son palier (resp. 95% de la valeur du palier.