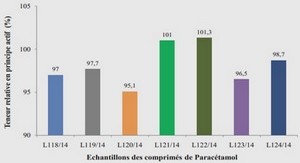
MÉTHODE NUMÉRIQUE POUR L’ÉQUATION DE
BURGERS NON VISQUEUSE

Solutions régulières et méthode des caractéristiques

 Définition 2.1.1.

 La fonction u(t, x) est solution au sens classique de l’équation de Burgers non visqueuse si u est de classe C 1 en x et en t et satisfait (2.2). Pour résoudre l’équation (2.2) dans le cas scalaire on utilise la méthode des caractéristiques. Une caractéristique est une courbe (t, x(t)) le long de laquelle la solution de (2.2) est constante. Supposons que la donnée initiale u0 est suffisamment régulière par exemple de classe C 1 . Alors l’hypothèse de régularité sur u nous permet de remplacer la loi de conservation par l’équation non conservative : ∂tu + a(u)∂xu = 0 où a(u) = f 0 (u) Les caractéristiques sont des courbes du plan (t, x) données par :  x 0 (t) = a(u(t, x(t))) x(0) = x0 où x0 est le pied de la caractérisation à t = 0, un calcul immédiat donne : d dtu(t, x(t)) = ∂tu + x 0 (t)∂xu = ∂tu + a(u)∂xu = 0 .Ce qui montre que la solution u est constante le long d’une caractéristique. Cette méthode permet aussi de construire une solution régulière au problème de cauchy tant que deux caractéristiques ne se coupent pas. La solution est donnée par : u(x, t) = u0(ξ), avec x = ξ + a(u0(ξ))t

 Solutions faibles

 Même dans le cas où la fonction de flux f et la solution initiale sont régulières, il peut apparaître des discontinuités et des solutions non régulières. Les solutions de la loi de conservation scalaire (2.2) ne sont pas nécessairement de classe C 1 . Dans le cas où f est non linéaire et dans des conditions décrites dans [1], les courbes caractéristiques se coupent en un temps T ∗ (voir figure 2.1), et la méthode des caractéristiques cesse de fonctionner, ce cas correspond à l’apparition de singularités dans la solution de l’équation de convection (ondes de choc). Le temps critique est donné par la méthode des caractéristique : T ∗ = − 1 min(α, 0), α = miny∈R d dy f 0 (u0(y)) Ceci nécessite d’introduire la notion de la solution faible, initié par P.D. Lax [2]. Le principe de la notion de la solution faible est de multiplier (2.2) par une fonction test suffisamment régulière et d’intégrer sur un domaine arbitraire du plan (x, t) puis d’utiliser la formule d’intégration par parties pour faire disparaître les dérivées sur la solution. Dans la suite on donne la définition de la solution de l’équation (2.2) au sens des distributions. Définition 2.2.1. On appelle solution au sens des distributions une fonction u(t, x) solution de (2.2) telle que pour toute fonction test ϕ ∈ C ∞ 0 (R + ∗ R) on a : − ˆ +∞ 0 ˆ +∞ −∞ [ϕtu + ϕxf(u)]dxdt = ˆ +∞ −∞ ϕ(0, x)u(0, x)dx La motivation de cette définition provient du fait que les solutions classiques sont eux même des solutions au sens des distributions. On utilise simplement la formule d’intégration par parties (les termes de bords sont nuls puisque les fonctions tests sont à support compact). Notre objectif est de trouver des solutions qui ne sont pas nécessairement différentiables au sens classique ni même continue. Proposition 2.2.1. Soit u ∈ C 1 ([0, ∞[∗R) est une solution au problème (2.2) au sens classique, alors c’est une solution faible. Figure 2.1 – Caractéristiques issues de x− et x+ Preuve :soit u une fonction régulière du problème (2.2), on a alors : ∂tu(t, x) + ∂x(f(u(t, x))) = 0 Soit ϕ ∈ C ∞ c ([0, ∞[∗R), on a : ˆ +∞ 0 ˆ +∞ −∞ (∂tu(t, x) + ∂x(f(u(t, x)))ϕ(t, x)dxdt = 0 ⇔ ˆ +∞ 0 ˆ +∞ −∞ (∂tu(t, x)ϕ(x, t)dxdt + ˆ +∞ 0 ˆ +∞ −∞ ∂x(f(u(t, x)))ϕ(t, x)dxdt = 0 Les fonctions u ∈ C 1 ([0, ∞[∗R), f est de classe C 1 et ϕ est de classe C ∞ à support compact, donc ϕ∂tu et ϕ∂x(f(u)) sont continues et à support compact, donc de modules intégrables. On peut donc appliquer le théorème de Fubini : ˆ +∞ −∞ ( ˆ +∞ 0 ϕ(t, x)∂tu(t, x)dt)dx + ˆ +∞ 0 ( ˆ +∞ −∞ ϕ(t, x)∂x(f(u(t, x)))dx)dt = 0 En effectuant une intégration par partie on obtient : ˆ +∞ −∞ ([uϕ] +∞ 0 − ˆ +∞ 0 u(t, x)∂tϕ(t, x)dt)dx+ ˆ +∞ 0 ([f(u(t, x))ϕ(t, x)]+∞ −∞)− ˆ +∞ −∞ f(u(t, x))∂xϕdt ˆ +∞ −∞ u(0, x)ϕ(0, x)dx+ ˆ +∞ −∞ ˆ +∞ 0 u(t, x)∂tϕ(t, x)dtdx+ ˆ +∞ 0 ˆ +∞ −∞ f(u(t, x))∂xϕ(t, x)dxdt = 0 On a : ˆ +∞ 0 ˆ +∞ −∞ (u(t, x)∂tϕ(t, x) + f(u(t, x))∂xϕ(t, x))dtdx + ˆ +∞ −∞ u0(x)ϕ(0, x)dx = 0 D’après la définition précédente u est bien solution du problème (2.2). Réciproquement on a : Proposition 2.2.2. Soit u solution faible du problème (2.2). Si de plus, u ∈ C 1 ([0, ∞[∗R), alors u est solution (2.2) au sens classique. Preuve : soit u une solution faible du problème (2.2). On a u0 ∈ L 1 loc (R) et u ∈ L 1 olc ([0, ∞[∗R) u C 1 ([0, +∞[∗R). Soit ϕ ∈ C ∞ c ([0, +∞[∗R), on a : ˆ +∞ 0 ˆ +∞ −∞ (u(t, x)∂tϕ + f(u(t, x))∂xϕ(t, x))dtdx + ˆ +∞ −∞ u0(x)ϕ(0, x)dx = 0 Prenons ψ à support compact dans ]0, +∞[∗R alors ψ(0, x) = 0. On a donc ˆ +∞ 0 ˆ +∞ −∞ (u(t, x)∂tψ(t, x) + f(u(t, x))∂xψ(t, x))dtdx = 0 En appliquant Fubini et l’intégration par partie, on obtient : ˆ +∞ −∞ ˆ +∞ 0 ψ(t, x)∂tu(t, x)dtdx + ˆ +∞ 0 ˆ +∞ −∞ ψ(t, x)∂xf(u(t, x))dxdt = 0 On a : ˆ +∞ −∞ ˆ +∞ 0 (∂tu(t, x) + ∂xf(u(t, x)))ψ(x, t)dxdt = 0 Ceci est vrai pour tout ψ ∈ C ∞ c (R∗]0, +∞[), donc ∂tu(t, x) + ∂xf(u(t, x)) = 0 presque partout sur R + ∗ R. Or f est de classe C 1 , u est de classe C 1 donc (t, x) :→ ∂tu(t, x) + ∂xf(u(t, x)) est continue. Il en résulte que : ∂tu(t, x) + ∂xf(u(t, x)) = 0 sur R + ∗ R Prenons maintenant ϕ ∈ C ∞ c (R∗]0, +∞[) ˆ +∞ 0 ˆ +∞ −∞ (u(t, x)∂tϕ(t, x) + f(u(t, x))∂xϕ(t, x))dtdx + ˆ +∞ −∞ u0(x)ϕ(0, x)dx = 0 Par intégration par partie et l’application du théorème de Fubini, on obtient : − ˆ +∞ −∞ u(0, x)ϕ(0, x)dx + ˆ +∞ 0 ˆ +∞ −∞ (∂tu(t, x) + ∂xf(u(t, x)))ϕ(t, x)dxdt + ˆ +∞ −∞ u0(x)ϕ(0, x)dx = 0 Soit : ˆ +∞ −∞ (u(0, x) − u0(x))ϕ(0, x)dx = 0 Ceci est vrai pour tout ϕ ∈ C ∞ c (R ∗ [0, +∞[) et l’application : x → u(0, x) − u0(x) est continue, donc : u(0, x) − u0(x) = 0 sur R Ainsi, on a bien u(0, x) = u0(x), ∀x ∈ R. Théorème 2.2.1. Pour tout T > 0 et toute donnée initiale u0 ∈ L ∞(R) u C 1 (R), il existe au moins une solution faible u ∈ L ∞(]0, T[∗R) au problème :  ∂tu(t, x) + ∂x(f(u(t, x))) = 0∀t ∈]0, T[, ∀x ∈ R u(0, x) = u0(x) Non-unicité de la solution faible et condition d’entropie xi 2.3 Relation de Rankine-Hugoniot Si une solution faible présente des discontinuités, nous pouvons tirer de la définition 2.2.1 une relation appelée relation de saut ou de Rankine-Hugoniot. On suppose que u est de classe C 1 sauf sur une ligne de discontinuité Γ paramétrée par (t, x(t)). On note ug et ud les valeurs de u de part et d’autre de la discontinuité et [u] = ud − ug le saut de u à travers la continuité (voir figure 2.2). 

Relation de Rankine-Hugoniot

oit u une solution de (2.2) discontinue suivant une trajectoire régulière Γ. La relation de saut s’écrit : [f(u)] = α[u], (2.3) où α = x 0 (t) est la vitesse de la discontinuité (vitesse de choc ou shock speed). Théorème 2.3.1 (1). Soit u une fonction de classe C 1 par morceau , alors u est une solution faible de (2.2) au sens des distributions si et seulement si 1. u est une solution classique de (2.2) quand elle est C 1 . 2. u satisfait la relation de saut 2.3 le long des discontinuités. Figure 2.2 – Solution discontinue le long d’une courbe 2.4 Non-unicité de la solution faible et condition d’entropie On montre que le problème (2.2) admet une solution faible qui n’est pas unique comme le montre l’exemple suivant. On considère l’équation de Burgers non visqueuse avec une condition initiale constante par morceaux, comme suit :    ∂u ∂t + ∂ ∂x ( u 2 2 ) = 0 u0(x) =  −1 si x < 0 1 si x ≥ 0 (2.4) Solutions entropiques : existence et unicité xii On peut construire au moins deux solutions faibles du problème (2.4). La première est celle qui reste égale à u0 pour tout t > 0, c’est à dire : u(t, x) =  −1 si x < 0 1 si x ≥ 0 En effet, u ∈ L ∞((0, T) ∗ R) et on a : ˆ T 0 ˆ 0 −∞ (u∂tϕ + f(u)∂ϕx)dxdt + ˆ 0 −∞ u0(x)ϕ(0, x)dx = ˆ T 0 f(−1)ϕ(t, 0)dt ˆ T 0 ˆ +∞ 0 (u∂tϕ + f(u)∂ϕx)dxdt + ˆ +∞ 0 u0(x)ϕ(0, x)dx = − ˆ T 0 f(1)ϕ(t, 0)dt En sommant ces deux égalités, on voit que u est solution faible puisque f(1) = f(−1). La deuxième solution est donner par : v(t, x) =    −1 si x t < −1 x t si −1 ≤ x t ≤ 1 1 si x t ≥ 1 On vérifie que v est aussi solution faible du problème de Burgers (2.4). La notion de solution faible ne suffit donc pas à déterminer la solution physiquement observée car elle n’est unique. Pour éliminer les solutions supplémentaires et pour que le problème d’évolution soit bien posé en présence d’un choc (c’est un autre nom pour ”discontinuité”), on doit ajouter une condition supplémentaire appelée condition d’entropie. Une solution du problème (2.2) est une onde de choc ou de raréfaction qui se propage avec la vitesse α et qui satisfait la condition d’entropie : f 0 (ud) < s < f0 (ug) (2.5) La justification mathématique de la notion d’entropie se fait dans la section suivante. 2.5 Solutions entropiques : existence et unicité Dans le cas scalaire, un théorème d’unicité de la solution faible vérifiant une condition d’entropie a été démontré par S.N. Krushkov[4]. L’existence de cette solution est obtenue par des méthodes de viscosités s’appuyant essentiellement sur la vérification du principe du maximum et sur une estimation de la variation totale. Cependant dans le cas général des systèmes (équation d’Euler par exemple) le problème reste ouvert bien qu’il existe néanmoins des résultats en dimension un. Dans le cas direct, des études analogues ont été menées pour définir et déterminer si un schéma numérique est entropique, c’est à dire s’il y a convergence vers une solution vérifiant une condition d’entropie. On citera par exemple les travaux de Leroux ([5]) sur les schémas de type Godunov et ceux d’Osher sur les E-schemas([6]). Définition 2.5.1. (solution entropique,[7]) Une fonction convexe η est appelée entropie de (2.2) s’il existe une fonction S appelée flux d’entropie telle que : η 0 (u)f 0 (u) = S 0 (u) (2.6) Une solution faible u de (2.2) est appelée solution entropie si pour toute entropie η de flux S du problème (2.2), u vérifie : ∂η(u) ∂t + ∂S(u) ∂x ≤ 0 (2.7) au sens des distributions. D’une manière alternative (2.7) s’écrit : ˆ +∞ 0 ˆ +∞ −∞ [ϕtη(u) + ϕxS(u)]dxdt ≤ − ˆ +∞ −∞ ϕ(0, x)η(u(0, x))d.