Modélisation stochastique de l’expression des gènes et
inférence de réseaux de régulation

Un modèle physique pour décrire les gènes en interaction

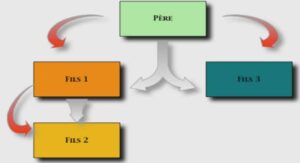
Dans ce chapitre nous allons construire un modèle dynamique de réseau de régulation, c’est-à-dire décrivant l’évolution temporelle des niveaux d’expression d’un ensemble de gènes potentiellement en interaction. Comme évoqué dans l’introduction, l’idée est de partir du diagramme de la Figure 1 tout en ajoutant la possibilité d’une rétroaction des protéines sur la transcription. Le résultat sera un processus stochastique – prenant la forme d’un système de particules en interaction – et nous adopterons tantôt le point de vue des trajectoires (modèle à base d’agents), tantôt celui, dual, de la distribution (équation maîtresse).

Expression d’un gène isolé

Avant d’envisager la modélisation d’un système aussi complexe qu’un réseau de gènes, il est nécessaire de s’intéresser à la dynamique individuelle de chaque gène. On a besoin d’un modèle assez sophistiqué pour décrire l’évolution des quantités qui nous intéressent (ARNm et protéines), mais également assez simple pour être accessible mathématiquement. Les modélisateurs se penchent depuis longtemps sur la dynamique stochastique des gènes et il existe aujourd’hui de nombreux modèles (Boettiger, 2013). Leur complexité est très variable mais ils ont en commun un formalisme mathématique hérité de la chimie, où la dynamique temporelle des molécules est décrite par des processus markoviens de type naissance-mort. Puisque l’expression d’un gène se résume à un ensemble (très grand) de réactions chimiques, l’idée est de choisir quelles réactions on souhaite décrire précisément.

Modèle standard

Notre point de départ est le modèle à deux états, 1 qui est rapidement devenu standard car c’est le plus simple qui soit capable de décrire l’expression d’un gène de manière satisfaisante à l’échelle de la cellule (Raser et O’Shea, 2004 ; Becskei et al., 2005 ; Raj et al., 2006 ; Suter et al., 2011). Il s’agit en fait de la version en temps continu d’une chaîne de Markov introduite par Ko (1991) sur la base d’expériences pionnières en cellules uniques (Ko et al., 1990). Dans ce modèle, un gène est décrit par son promoteur qui peut être soit « actif » (ON) soit « inactif » (OFF), représentant par exemple l’état de fixation sur l’ADN d’un complexe 1. Il est aussi appelé random telegraph dans la littérature de biologie : nous n’utiliserons pas ce nom ici afin d’éviter la confusion avec des homonymes issus d’autres communautés scientifiques.  Figure 1.1 – Diagramme classique du modèle à deux états. moléculaire d’initiation de la transcription. Le phénomène à l’origine de ces deux états peut être plus subtile (Larson, 2011 ; Chong et al., 2014), mais le principe essentiel est que le gène ne produit de l’ARNm que lorsque le promoteur est actif. On ajoute l’étape de traduction, ainsi que la dégradation de l’ARNm et des protéines, comme des réactions de premier ordre. Plus précisément, le modèle correspond aux réactions élémentaires suivantes : G kon −−→ G ∗ , G ∗ koff −−→ G G ∗ s0 −→ G ∗ + M, M s1 −→ M + P M d0 −→ ∅, P d1 −→ ∅ (1.1) où G, G ∗ , M et P désignent respectivement le promoteur inactif, le promoteur actif, l’ARNm et les protéines. Une représentation classique est le diagramme de la Figure 1.1. Celui-ci n’a pas vraiment de sens mathématiquement, mais il est souvent utilisé car il permet de décrire simplement les six réactions chimiques considérées ainsi que leurs taux (par molécule de chaque réactif) : chaque nœud correspond à une espèce et chaque flèche à une réaction. Dans toute la suite, on supposera que ces taux sont strictement positifs. Il nous faut maintenant un modèle mathématique pour décrire le système de réactions chimiques (1.1). Une des caractéristiques fondamentales est que les espèces considérées sont présentes en très petite quantité par rapport au nombre d’Avogadro, sans compter que G et G ∗ sont par définition des espèces rares puisque leurs nombres de molécules [G] et [G ∗ ] sont égaux à 0 ou 1 avec à tout instant [G] + [G ∗ ] = 1. L’option typique consiste alors à supposer que toutes les réactions élémentaires suivent la loi d’action des masses stochastique, ce qui correspond, en notant respectivement Et = [G ∗ ], Mt = [M] et Pt = [P] à l’instant t, à dire que (Et , Mt , Pt)t⩾0 est un processus markovien de sauts à valeurs dans S = {0, 1} × N × N dont le générateur L est donné, pour m, p ∈ N et f = (f0, f1) ⊤ : S → R, par Lf(m, p) = Qf(m, p) + S[f(m + 1, p) − f(m, p)] + s1m[f(m, p + 1) − f(m, p)] + d0m[f(m − 1, p) − f(m, p)] + d1p[f(m, p − 1) − f(m, p)] (1.2) avec S = ( 0 0 0 s0 ) et Q = ( −kon kon koff −koff ) . Il existe alors une méthode de construction très classique des trajectoires, que l’on rappelle ici. Étant donné (e, m, p) = (Et , Mt , Pt) ∈ S l’état du processus à l’instant t, on a six évènements 18 1.1 Expression d’un gène isolé possibles récapitulés dans le tableau suivant, indexés arbitrairement par i ∈ J1, 6K et pouvant chacun survenir de manière indépendante avec un taux λi . i Taux λi Interprétation État d’arrivée 1 kon(1 − e) Passage dans l’état actif (1 − e, m, p) 2 koffe Passage dans l’état inactif (1 − e, m, p) 3 s0e Création d’un ARNm (e, m + 1, p) 4 s1m Création d’une protéine (e, m, p + 1) 5 d0m Dégradation d’un ARNm (e, m − 1, p) 6 d1p Dégradation d’une protéine (e, m, p − 1) On construit alors la trajectoire de la façon suivante : l’état du processus reste égal à (e, m, p) jusqu’à l’instant t + T avec T aléatoire et distribué selon la loi exponentielle de paramètre λ = λ1 + · · · + λ6, puis à cet instant le processus change d’état aléatoirement et arrive avec probabilité pi = λi/λ dans l’état correspondant à l’évènement i. On réitère ensuite ce procédé à partir de t + T, et ainsi de suite jusqu’à passer un instant final donné. On peut vérifier que le processus (Et , Mt , Pt)t⩾0 ainsi construit est bien un processus de Markov dont le semi-groupe a pour générateur l’opérateur L défini par (1.2), ce qui constitue un exercice classique (Liggett, 2010). On remarque bien sûr que chaque évènement de saut correspond précisément à l’une des réactions du système (1.1), et il se trouve que cette méthode de construction correspond au célèbre algorithme de simulation moléculaire introduit par Gillespie (1977). Noter qu’un physicien ou un biologiste dira directement qu’il simule (1.1) par l’algorithme de Gillespie. Remarque 1.1. Dans le générateur (1.2), on a décrit M et P de manière traditionnelle mais on a « vectorisé » la notation pour G ∗ . Ce formalisme sera utilisé dans toute la suite et nous permettra de simplifier énormément les calculs. 1.1.2 Première simplification Le processus de sauts défini par (1.2) est la façon la plus classique de modéliser un système chimique en distinguant chaque molécule.2 En pratique, il n’est pas nécessaire de garder une description discrète pour M et P, qui sont des espèces abondantes et sans relation de conservation. Des expériences quantitatives (Schwanhäusser et al., 2011) suggèrent que les paramètres de création et dégradation vérifient typiquement s0 ≫ d0 et s1 ⩾ d1. Dans ce régime, l’échelle des niveaux d’ARNm et de protéines est assez grande pour qu’il semble tout à fait satisfaisant de négliger leur « bruit moléculaire » en les considérant comme des quantités continues qui suivent les équations différentielles associées à la loi d’action des masses classique (i.e. déterministe). On obtient le modèle hybride :    Et : 0 kon −−→ 1, 1 koff −−→ 0 M˙ t = s0Et − d0Mt P˙ t = s1Mt − d1Pt (1.3) en utilisant une notation intuitive empruntée à Rudnicki (2015). En d’autres termes, l’état du promoteur Et suit toujours le même processus markovien de sauts à deux états, mais l’ARNm 2. Pour une présentation générale du formalisme, on pourra par exemple consulter l’excellent et très concis Anderson et Kurtz (2015) où l’hypothèse prend le nom de stochastic mass-action kinetics.  Figure 1.2 – Exemple de trajectoires du modèle discret (gauche) et du modèle PDMP (droite), où l’on ne représente ici que l’état du promoteur (Et) et l’ARNm (Mt). Le fait de considérer la même trajectoire de Et permet de se rendre compte du lien entre les deux processus. De manière intuitive, la production des protéines sera alors très similaire dans les deux cas. Les valeurs des paramètres choisies pour cet exemple sont kon = 0.6, koff = 5, d0 = 1 et s0 = 200 (en h−1 ). et les protéines suivent maintenant des équations différentielles ordinaires dont la première dépend de Et (Figure 1.2). Ce modèle n’est autre qu’un processus de Markov déterministe par morceaux (PDMP) appartenant à la classe bien connue des switching ODEs (Benaïm et al., 2012, 2015). Il y a deux façons de le justifier mathématiquement : • On peut montrer que c’est bien la limite du modèle discret (1.2) dans le régime s0 ≫ d0 et s1 ⩾ d1, ce qui a été fait par Crudu et al. (2012). • On peut mettre en évidence un lien algébrique – donc exact – qui permet d’interpréter le PDMP comme la structure sous-jacente fondamentale du modèle discret. En particulier, une des conséquences probabilistes est que la trajectoire de l’ARNm provenant du PDMP apparaît comme l’espérance conditionnelle de son homologue dans le processus de sauts sachant la trajectoire du promoteur. Le deuxième point sera détaillé dans le chapitre 3 où il aura un rôle essentiel. On renvoie également à la Figure 1.2 et au chapitre 6 pour une comparaison numérique. Pour l’heure, disons simplement que le modèle (1.3) est bien justifié dans notre cas : c’est ce modèle qui va nous servir de brique de base pour construire un réseau de régulation. 1.1.3 Le régime « bursty » Lorsqu’à la fois kon ≪ koff et d0 ≪ koff, l’ARNm est produit par bursts, c’est-à-dire pendant de courtes périodes de temps telles que son niveau reste toujours très en dessous de la saturation s0/d0 (cf. Figure 1.2). La quantité produite lors d’un burst s’approche alors au premier ordre comme étant s0T où T est la durée du burst, qui suit par définition une loi exponentielle de paramètre koff. De plus, les périodes actives du promoteur sont bien plus courtes que les périodes inactives de sorte que les premières peuvent être vues comme instantanées, ce qui justifie l’appellation fréquence de burst pour kon qui est l’inverse de la durée moyenne de l’état inactif. Nous nous placerons dans ce régime dans toute la suite car c’est celui qui apparaît systématiquement dans les expériences (Raj et al., 2006 ; Suter et al., 2011 ; Viñuelas et al., 2013 ; Albayrak et al., 2016 ; Richard et al., 2016). Du point de vue mathématique (Crudu et al., 2012), il est possible d’effectuer directement le passage à la limite koff → +∞ à partir du modèle discret (1.2) en même temps que celui associé à s0 ≫ d0, qui s’écrit alors s0 → +∞ avec λ = koff/s0 fixé. L’état du promoteur n’a alors plus besoin d’être décrit puisque ses périodes d’activation sont infiniment courtes, et on obtient un nouveau processus (Mt , Pt)t⩾0 à valeurs dans S = R+ × R+ dont le générateur 

Expression d’un gène isolé

Figure 1.3 – Exemple de trajectoire du modèle PDMP bursty. Les valeurs des paramètres choisies sont kon = 0.6, koff = 5, d0 = 1, d1 = 0.2, s0 = 200 et s1 = 400 (en h−1 ), le but étant d’obtenir des quantités réalistes d’ARNm et de protéines (Albayrak et al., 2016). est donné par Lf(m, p) = kon ∫ ∞ 0 [f(m + y, p) − f(m, p)]λe−λydy − d0m∂mf(m, p) + (s1m − d1p)∂pf(m, p) (1.4) pour f : S → R de classe C 1 et (m, p) ∈ S. Il s’agit encore d’un PDMP, mais cette fois les sauts affectent directement le flot de l’équation différentielle et la trajectoire de Mt peut être choisie càdlàg mais pas continue. La construction d’une trajectoire se fait comme suit : étant donné (m, p) = (Mt , Pt) ∈ S l’état à l’instant t, le processus suit la dynamique déterministe donnée par { M˙ t = −d0Mt P˙ t = s1Mt − d1Pt jusqu’à l’instant t+T avec T distribué selon la loi exponentielle de paramètre kon, puis à cet instant la première composante saute d’une hauteur Y (i.e. on pose Mt+T = M− t+T + Y où M− t+T est la limite à gauche de s 7→ Ms en t+T) avec Y distribuée selon la loi exponentielle de paramètre λ. On répète alors ces deux étapes à partir de t + T, et ainsi de suite (Figure 1.3). Remarquons finalement qu’il existe une variante assez populaire qui modélise seulement les protéines, de la même façon que l’ARNm ici (Friedman et al., 2006 ; Mackey et al., 2011 ; Pájaro et al., 2017), avec une généralisation possible de la loi des hauteurs de saut. Nous n’utiliserons pas le modèle (1.4) dans la suite car il n’apporte pas réellement de simplification par rapport à (1.3) pour les problèmes qui nous intéressent, mais le régime bursty sera quand même intéressant à avoir en tête pour les applications. Par ailleurs, nous verrons que les résultats du chapitre 2 s’adaptent naturellement à ce régime limite.